Задача о характере поля тяготения в сферически-симметричном случае с учетом эффектов общей теории относительности сразу же после опубликования классической работы Эйнштейна была точно решена выдающимся немецким астрофизиком К. Шварцшильдом (отцом ныне здравствующего профессора М. Шварцшильда, так много сделавшего для теории эволюции звезд). Пользуясь решением К. Шварцшильда, можно найти зависимость радиуса коллапсирующей звезды от времени так, как это представляется по часам «внешнего» (например, земного) наблюдателя:
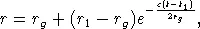 |
(24.1) |
где r g = 2 GM/c 2 — так называемый «гравитационный радиус», а сфера радиуса r g называется «сферой Шварцшильда». Заметим, что для Солнца r g = 2 , 96 км, а для Земли r g = 0 , 44 см, r 1 — радиус звезды в момент t 1, причем в формуле (24.1) предполагается, что ( r 1- r g ) 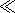 r g . Напомним, что радиусы нейтронных звезд только в несколько раз больше их гравитационного радиуса. Применение решения К. Шварцшильда к проблеме коллапса невращающейся звезды вполне законно, так как мы можем рассматривать движение каждой точки на поверхности коллапсирующей звезды как свободное падение в сферически-симметричном поле тяготения. Из формулы (27), таким образом, следует, что с точки зрения внешнего наблюдателя при приближении r к r g скорость сжатия асимптотически замедлится практически до нуля. Внешний наблюдатель никогда не зафиксирует переход сжимающейся звезды под сферу Шварцшильда — ведь по его часам для этого сжимающейся звезде потребуется бесконечно большое время. А между тем воображаемый наблюдатель, находящийся на сжимающейся звезде и коллапсирующий вместе с ней, никаких особенностей, связанных с пересечением сферы Шварцшильда, не заметит. По его часам пройдут считанные секунды, в течение которых звезда и он сам сожмутся в точку. Здесь эффекты общей теории относительности проявляют себя самым разительным образом. Грубо говоря, смысл этих эффектов состоит в том, что в очень сильном гравитационном поле скорость течения всех процессов (по часам внешнего наблюдателя) крайне замедляется.
r g . Напомним, что радиусы нейтронных звезд только в несколько раз больше их гравитационного радиуса. Применение решения К. Шварцшильда к проблеме коллапса невращающейся звезды вполне законно, так как мы можем рассматривать движение каждой точки на поверхности коллапсирующей звезды как свободное падение в сферически-симметричном поле тяготения. Из формулы (27), таким образом, следует, что с точки зрения внешнего наблюдателя при приближении r к r g скорость сжатия асимптотически замедлится практически до нуля. Внешний наблюдатель никогда не зафиксирует переход сжимающейся звезды под сферу Шварцшильда — ведь по его часам для этого сжимающейся звезде потребуется бесконечно большое время. А между тем воображаемый наблюдатель, находящийся на сжимающейся звезде и коллапсирующий вместе с ней, никаких особенностей, связанных с пересечением сферы Шварцшильда, не заметит. По его часам пройдут считанные секунды, в течение которых звезда и он сам сожмутся в точку. Здесь эффекты общей теории относительности проявляют себя самым разительным образом. Грубо говоря, смысл этих эффектов состоит в том, что в очень сильном гравитационном поле скорость течения всех процессов (по часам внешнего наблюдателя) крайне замедляется.
С точки зрения внешнего наблюдателя в процессе гравитационного коллапса светимость звезды при приближении ее радиуса к гравитационному будет катастрофически быстро падать. Это падение светимости обусловлено совместным действием гравитационного красного смещения, эффекта Доплера и аберрации света. На основе теории К. Шварцшильда можно получить следующее выражение для зависимости светимости коллапсирующей звезды от времени:
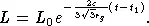 |
(24.2) |
В пределе при t 
 светимость L
светимость L  0, так же как и частота излучения. Для наблюдателя же, связанного с коллапсирующей звездой, светимость (по его часам!) может даже расти. С точки зрения же внешнего наблюдателя коллапсирующая звезда практически перестанет излучать и прекратит свое сжатие у r
0, так же как и частота излучения. Для наблюдателя же, связанного с коллапсирующей звездой, светимость (по его часам!) может даже расти. С точки зрения же внешнего наблюдателя коллапсирующая звезда практически перестанет излучать и прекратит свое сжатие у r  r g за время (по его часам!)
r g за время (по его часам!)  r g /c , т. е.
r g /c , т. е.  10 -5с. Сказанное относится не только к фотонному, но и к нейтринному излучению коллапсирующей звезды. Как показал В. Л. Гинзбург, магнитное поле коллапсирующей звезды при r
10 -5с. Сказанное относится не только к фотонному, но и к нейтринному излучению коллапсирующей звезды. Как показал В. Л. Гинзбург, магнитное поле коллапсирующей звезды при r  r g также как бы исчезает для внешнего наблюдателя.
r g также как бы исчезает для внешнего наблюдателя.
Таким образом, для внешнего наблюдателя за очень короткое время  10 -5с коллапсирующая звезда как бы «пропадает». Такой объект получил весьма образное название «черной дыры». Никакое излучение — фотонное, нейтринное или корпускулярное,— из такой «дыры» уже не выходит. Единственное, что остается от этой звезды для внешнего мира,— это ее гравитационное поле, определяемое массой. Если, например, в двойной системе одна из компонент сколлапсирует, то это ничуть не отразится на движении второй компоненты.
10 -5с коллапсирующая звезда как бы «пропадает». Такой объект получил весьма образное название «черной дыры». Никакое излучение — фотонное, нейтринное или корпускулярное,— из такой «дыры» уже не выходит. Единственное, что остается от этой звезды для внешнего мира,— это ее гравитационное поле, определяемое массой. Если, например, в двойной системе одна из компонент сколлапсирует, то это ничуть не отразится на движении второй компоненты.
Читать дальше

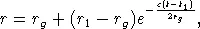
 r g . Напомним, что радиусы нейтронных звезд только в несколько раз больше их гравитационного радиуса. Применение решения К. Шварцшильда к проблеме коллапса невращающейся звезды вполне законно, так как мы можем рассматривать движение каждой точки на поверхности коллапсирующей звезды как свободное падение в сферически-симметричном поле тяготения. Из формулы (27), таким образом, следует, что с точки зрения внешнего наблюдателя при приближении r к r g скорость сжатия асимптотически замедлится практически до нуля. Внешний наблюдатель никогда не зафиксирует переход сжимающейся звезды под сферу Шварцшильда — ведь по его часам для этого сжимающейся звезде потребуется бесконечно большое время. А между тем воображаемый наблюдатель, находящийся на сжимающейся звезде и коллапсирующий вместе с ней, никаких особенностей, связанных с пересечением сферы Шварцшильда, не заметит. По его часам пройдут считанные секунды, в течение которых звезда и он сам сожмутся в точку. Здесь эффекты общей теории относительности проявляют себя самым разительным образом. Грубо говоря, смысл этих эффектов состоит в том, что в очень сильном гравитационном поле скорость течения всех процессов (по часам внешнего наблюдателя) крайне замедляется.
r g . Напомним, что радиусы нейтронных звезд только в несколько раз больше их гравитационного радиуса. Применение решения К. Шварцшильда к проблеме коллапса невращающейся звезды вполне законно, так как мы можем рассматривать движение каждой точки на поверхности коллапсирующей звезды как свободное падение в сферически-симметричном поле тяготения. Из формулы (27), таким образом, следует, что с точки зрения внешнего наблюдателя при приближении r к r g скорость сжатия асимптотически замедлится практически до нуля. Внешний наблюдатель никогда не зафиксирует переход сжимающейся звезды под сферу Шварцшильда — ведь по его часам для этого сжимающейся звезде потребуется бесконечно большое время. А между тем воображаемый наблюдатель, находящийся на сжимающейся звезде и коллапсирующий вместе с ней, никаких особенностей, связанных с пересечением сферы Шварцшильда, не заметит. По его часам пройдут считанные секунды, в течение которых звезда и он сам сожмутся в точку. Здесь эффекты общей теории относительности проявляют себя самым разительным образом. Грубо говоря, смысл этих эффектов состоит в том, что в очень сильном гравитационном поле скорость течения всех процессов (по часам внешнего наблюдателя) крайне замедляется.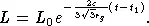

 светимость L
светимость L  0, так же как и частота излучения. Для наблюдателя же, связанного с коллапсирующей звездой, светимость (по его часам!) может даже расти. С точки зрения же внешнего наблюдателя коллапсирующая звезда практически перестанет излучать и прекратит свое сжатие у r
0, так же как и частота излучения. Для наблюдателя же, связанного с коллапсирующей звездой, светимость (по его часам!) может даже расти. С точки зрения же внешнего наблюдателя коллапсирующая звезда практически перестанет излучать и прекратит свое сжатие у r  r g за время (по его часам!)
r g за время (по его часам!)  r g /c , т. е.
r g /c , т. е.  10 -5с. Сказанное относится не только к фотонному, но и к нейтринному излучению коллапсирующей звезды. Как показал В. Л. Гинзбург, магнитное поле коллапсирующей звезды при r
10 -5с. Сказанное относится не только к фотонному, но и к нейтринному излучению коллапсирующей звезды. Как показал В. Л. Гинзбург, магнитное поле коллапсирующей звезды при r  r g также как бы исчезает для внешнего наблюдателя.
r g также как бы исчезает для внешнего наблюдателя. 10 -5с коллапсирующая звезда как бы «пропадает». Такой объект получил весьма образное название «черной дыры». Никакое излучение — фотонное, нейтринное или корпускулярное,— из такой «дыры» уже не выходит. Единственное, что остается от этой звезды для внешнего мира,— это ее гравитационное поле, определяемое массой. Если, например, в двойной системе одна из компонент сколлапсирует, то это ничуть не отразится на движении второй компоненты.
10 -5с коллапсирующая звезда как бы «пропадает». Такой объект получил весьма образное название «черной дыры». Никакое излучение — фотонное, нейтринное или корпускулярное,— из такой «дыры» уже не выходит. Единственное, что остается от этой звезды для внешнего мира,— это ее гравитационное поле, определяемое массой. Если, например, в двойной системе одна из компонент сколлапсирует, то это ничуть не отразится на движении второй компоненты.




![Андрэ Нортон - Рожденные среди звезд [= Рождение звезды]](/books/322400/andre-norton-rozhdennye-sredi-zvezd-rozhdenie-zve-thumb.webp)
![Эдвард Радзинский - Тираны России и СССР [Распутин. Жизнь и смерть + Сталин. Жизнь и смерть]](/books/391099/edvard-radzinskij-tirany-rossii-i-sssr-rasputin-thumb.webp)


