Айзек Азимов - Нейтрино - призрачная частица атома

Вообразите бильярдный шар, движущийся по поверхности стола самым простым образом, без каких-либо вращений, с постоянной скоростью 10 см/сек. Предположим далее, что этот бильярдный шар налетает на неподвижный, который тотчас начинает двигаться, а первый останавливается. При этом, если столкновение было центральным, второй бильярдный шар движется со скоростью 10 см/сек точно в том же направлении, в каком двигался раньше первый. Многочисленными наблюдениями установлено, что при таком столкновении сумма скоростей шаров до и после соударения одинакова (на самом деле имеется небольшое замедление из-за трения шара о поверхность стола и сопротивления окружающего воздуха но этими эффектами пока можно пренебречь). Короче, общая скорость остается неизменной, в то время как другие факторы, например положение и скорость каждого шара в отдельности, меняются. Казалось бы, общая скорость «сохраняется».

Значение такого обобщения в том, что оно исключает все виды случайностей из области возможного. Вы можете быть уверены, что ни один шар не будет двигаться быстрее определенного предела. Более того, если в такой системе из двух шаров известна скорость одного шара тем самым уже предопределена скорость другого. Но будет ли общая скорость «сохраняться» во всех случаях или только в том, который я только что описал?

Что будет, например, если шар ударит не покоящийся, а движущийся шар? Предположим, что один бильярдный шар движется со скоростью 10 см/сек, скажем, на север, другой — со скоростью 10 см/сек на юг, и оба они сталкиваются «в лоб». Мы полагаем, что шары в этих условиях отскочат друг от друга. Но что произойдет, если шары сделать из воска или замазки, так что при соударении они сплющатся и прилипнут друг к другу? Остановятся ли шары в точке столкновения и какими в этом случае будут их скорости?

Конечно, если скорость исчезает, вряд ли можно говорить, что она сохраняется, Чтобы говорить о сохранении скорости, необходимо, оказывается, рассматривать не только ее величину, но и направление движения предмета. Предположим, что скорость движения шара на север равна +10 см/сек, а скорость движения на юг -10 см/сек. В таком случае общая скорость двух движущихся шаров равна не 20 см/сек, а нулю. Следовательно, если два неупругих шара сталкиваются, прилипают и останавливаются в точке столкновения, никакого изменения суммарной скорости не происходит. Нуль остается нулем.

В случае настоящих упругих бильярдных шаров ситуация иная. Каждый шар внезапно меняет направление движения. Шар, движущийся на север, отскакивает на юг, причем скорость его меняется от +10 см/сек до -10 см/сек. Второй шар отскакивает на север, и скорость его меняется от -10 см/сек до +10 см/сек. Однако суммарная скорость остается равной нулю. Если шары недостаточно упруги, то может случиться, что один шар изменит скорость от +10 см/сек до -6 см/сек. Тогда другой изменит скорость с -10 см/сек до +6 см/сек. Результатов такого центрального столкновения множество, но они ограничены условием обязательного сохранения суммарной скорости.

Однако можно усложнить задачу. Что если движущийся бильярдный шар ударяет неподвижный, но не по центру? Что тогда?

Если вы когда-нибудь следили за игрой в бильярд, вы знаете ответ на этот вопрос: шары меняют направление. Неподвижный шар начинает двигаться налево (если удар был справа от центра), а шар, двигавшийся вначале, тоже меняет направление и начинает двигаться направо. При этом никогда не наблюдалось, чтобы оба шара двигались в одну сторону с первоначальным направлением.

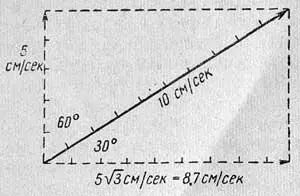
Рис. 1. Разложение скорости

Рассмотрим прямолинейное движение в двух измерениях (скажем, на плоской поверхности бильярдного стола). Такое движение всегда можно разложить на две составляющие под прямым углом друг к другу. Это делается с помощью построения линий в направлении движения, длины которых пропорциональны величинам скоростей (рис. 1). Величины горизонтальной и вертикальной составляющих скорости можно определить, составив отношение длин сторон прямоугольника к его диагонали. Это отношение можно вычислить, если известны углы геометрической фигуры. Мы не будем касаться таких расчетов, тем не менее рис. 1 как раз соответствует простому случаю, когда прямолинейное движение со скоростью 10 см/сек имеет вертикальную составляющую 5 см/сек и горизонтальную 8,7 см/сек [1] [1] Аналогичное рассмотрение проводится и в трехмерном пространстве, где прямолинейное движение можно разложить на три взаимно перпендикулярные составляющие. Каждая составляющая скорости будет пропорциональна длине одной из трех сторон куба диагональю которого является скорость начального движения. .