Владимир Секерин - Теория относительности — мистификация ХХ века

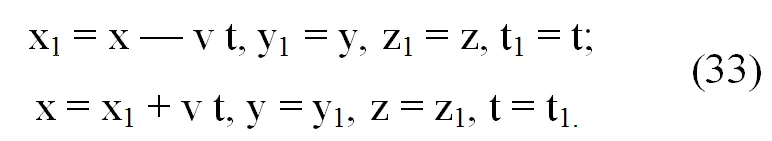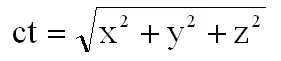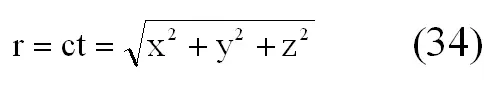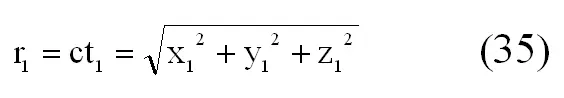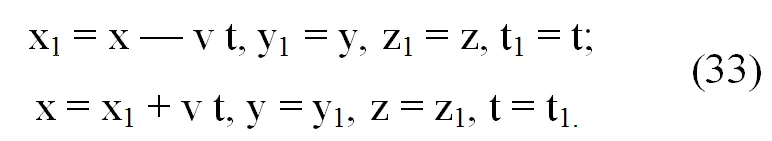
Эти уравнения описывают координаты и время одного и того же точечного тела в системе отсчета Oxyzt — условно неподвижной, и O 1x 1y 1z 1t 1— движущейся относительно первой вдоль оси Ох со скоростью v. Время отсчитывается от момента совпадения О и О 1.

Согласуясь с принципом относительности Галилея, Ньютон ввел понятия абсолютного, истинного, пространства и абсолютного, истинного, времени, являющегося неизменными безотносительно к чему-либо. Меры этих величин — расстояние между двумя точками прямой и интервал времени между двумя событиями в инерциальных системах — неизменные, они носят название инвариантов преобразований Галилея.

Действительно, возьмем отрезок прямой — Δх и интервал времени — Δt в системе O, и равные им — Δx 1и Δt 1в системе О 1. Затем системе О 1придадим скорость v 1 v. В движущейся системе O 1,согласно принципу относительности Галилея, невозможно определить опытным путем новое инерциальное состояние по сравнению с прежним. Из этого следует, что отрезок прямой Δx 1и интервал времени Δt 1остаются прежними и равными Δx и Δt.

В качестве иллюстрации проявления принципа относительности Галилея рассмотрим необходимый в дальнейшем изложении пример. Представим две системы отсчета: неподвижную, условную, Oxyzt, и движущуюся относительно первой вдоль оси Ох со скоростью v, O 1x 1y 1z 1t 1. Направление соответствующих осей совпадает, (рис. 15, а). В момент совмещения начала координат в точке ОО 1происходит вспышка света. Если этот момент принять за начало отсчета времени, то положение фронта распространения света в момент времени t будет описываться уравнением сферы радиуса r равного

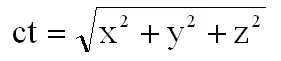
с центром в точке О, если источник был неподвижен относительно системы Oxyzt в момент вспышки. Относительно же центра О 1скорость света по оси х равна разности (с – V). И наоборот, если источник был неподвижен относительно системы O 1x 1y 1z 1t 1, то центр сферы будет находиться в точке О 1, а относительно О скорость света по оси х равна сумме (с + v), (рис. 15, б).

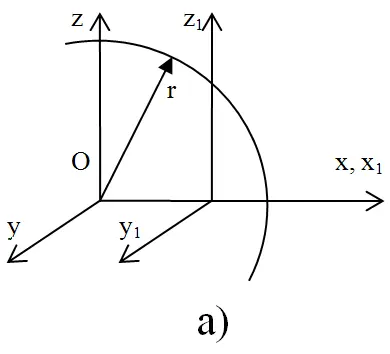
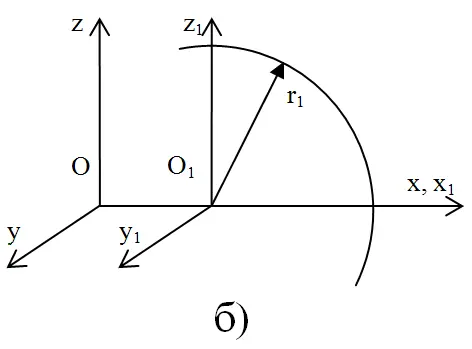
Рис. 15

Типичное изложение первого постулата теории относительности следующее: механические, оптические и электромагнитные явления во всех инерциальных системах отсчета протекают одинаково [3, 305].

Но изложенная формулировка маскировочная, в постулате заложен совсем иной смысл, чем тот, что дан в определении. Вводя в теорию второй постулат, Эйнштейн приходит в противоречие с принципом относительности Галилея, который несовместим с постулатом с = const. Несовместимость наглядно доказывается следующим образом.

Вернемся к примеру, изображенному на рис. 15. При тех же условиях в момент совпадения начала координат происходит вспышка света (рис. 16), этот момент принимаем за начало отсчета времени.

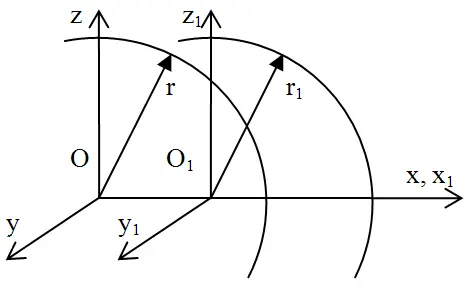
Рис. 16

Теперь, не учитывая, где находятся источник в системе О, или О 1, так как в обеих системах скорость света от одного и того же источника согласно постулату с = const равна с, имеем, что с одной стороны, положение фронта распространения света в момент времени t будет описываться уравнением сферы радиуса

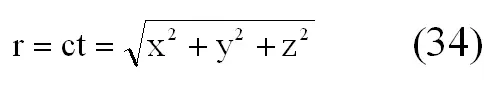
с центром в точке О, с другой стороны, фронт распространения света в момент времени t 1будет описываться уравнением сферы радиуса

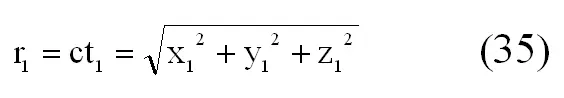
с центром в точке О 1. Таким образом, в один и тот же момент времени t = t 1фронт распространения света достигнет различных точек пространства, что лишено смысла.

Создавшееся противоречие Эйнштейн решает отказом от понятий абсолютного, истинного, пространства и абсолютного, истинного, времени Ньютона и введением сформулированных А. Пуанкаре и Г. Лоренцем понятий относительного пространства и относительности одновременности. Этим нововведением производится замена принципа относительности Галилея совсем другим принципом, согласно которому в инерциальных системах отсчета, движущихся относительно наблюдателя, процессы природы протекают уже иначе. Преобразование координат и времени принципа относительности Эйнштейна, записанные в виде уравнений, описывающих координаты и время одного и того же точечного тела в системах, движущихся одна относительно другой со скоростью v по оси Ох, имеют вид: