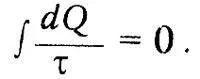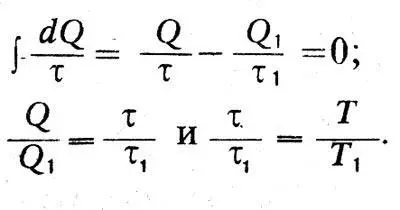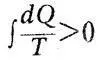Кудрявцев Степанович - Курс истории физики

Переходя ко второму началу термодинамики, Клаузиус рассматривает круговые обратимые процессы и указывает, что в простом круговом процессе типа цикла Карно совершаются два вида превращений: переход теплоты в работу и переход теплоты более высокой температуры в теплоту более низкой температуры. Второе начало «должно выражать отношение между этими двумя превращениями». Оба эти превращения — «явления одинаковой природы» и в обратимом процессе могут замещать друг друга. Клаузиус формулирует второе начало как принцип эквивалентности превращения следующим образом:

«Если мы назовем эквивалентными два превращения, которые могут замещать друг друга, не требуя для этого никакого другого длительного измене- , ния, то возникновение из работы количества теплоты Q, имеющего температуру Т, обладает эквивалентом Q/τ, а переход количества теплоты Q от температуры T1, к температуре Т2 имеет эквивалент Q (1/τ 2-1/τ 1), где τ есть некоторая функция температуры, независимая от рода процесса, с помощью которого совершаются превращения». Клаузиус показывает, что для обратимого кругового процесса сумма эквивалента равна нулю:

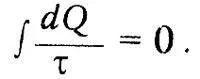
Это, по Клаузиусу, является математическим выражением второго начала. «Стоящее под знаком интеграла выражение dQ/τ, — пишет Клаузиус, —является дифференциалом некоторой связанной с состоянием тела величины, которая полностью определена, если известно состояние тела в рассматриваемый момент, хотя бы ничего не было известно о пути, по которому тело в рассматриваемое состояние пришло». Эту функцию Клаузиус ввел в 1865 г. и назвал энтропией (от греческого слова «тропэ»— превращение). Дифференциал энтропии

dS=dQ/τ.

Для определения функции температуры τ Клаузиус рассматривает обратимый процесс с идеальным газом. В этом случае отношение отданной и поглощенной теплоты Q и Q, будет равно отношению температур:

Q/Q1=T/T1. С другой стороны,

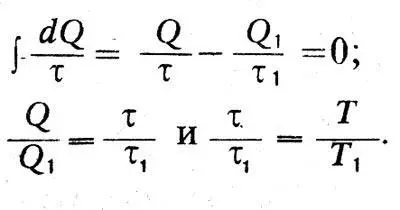
Следовательно,

<���τ/T = const.

Постоянная не имеет существенного значения. Принимая ее равной 1, получим τ=T и dS=dQ/T.

Для необратимых процессов

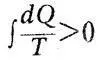
и энергия, способная к превращениям, уменьшается, а энтропия соответственно растет. Клаузиус формулирует второе начало термодинамики в виде положения: «Энтропия Вселенной стремится к максимуму». Так через 20 лет после Томсона Клаузиус также пришел к концепции «тепловой смерти». Постулат Клаузиуса и концепция тепловой смерти вызвали большое количество возражений. Были придуманы многочисленные эксперименты, казалось, противоречащие принципу Карно -Клаузиуса. Очень тонкий мысленный эксперимент выдвинул Максвелл в своей «Теории тепла» (1870). Максвелл сначала считал, что второе начало имеет ограниченную область применения. «Это положение, — писал Максвелл о втором начале, — несомненно верно, пока мы имеем дело с телами большой массы и не имеем возможности ни различать отдельных молекул в этих массах, ни работать с ними. Но если представить себе существо со столь изощренными способностями, что оно было бы в состоянии следить за каждой отдельной молекулой во всех ее движениях, то подобное существо было бы способно сделать то, что для нас в настоящее время невозможно... Представим себе..., что какой-нибудь сосуд разделен на две части А и В перегородкой с маленьким отверстием в ней. Пусть существо, способное различать отдельные молекулы, попеременно то открывает, то закрывает отверстие, и притом таким образом, чтобы только быстро движущиеся могли переходить из Л в Б, и только медленнее движущиеся, наоборот, из В в А: Следовательно, такое существо без затраты работы повысит температуру в В и понизит ее в А — вопреки второму началу термодинамики ».

«Демон Максвелла» работает, используя основные положения кинетической теории, согласно которым молекулы движутся с различными скоростями и температура пропорциональна средней кинетической энергии молекул. Действительно, молекулярная теория допускает существование процессов, происходящих в противоречии со вторым началом, а само второе начало является не абсолютным, а статистическим законом. «Демон Максвелла» -веха на пути к статистическому пониманию второго закона. Однако порожденная этим образом дискуссия привела к пониманию, что законы микро мира делают невозможным осущест вление эксперимента Максвелла.