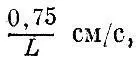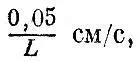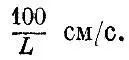Лев Ландау - Физика для всех. Молекулы

Но вернемся к законам "мокрого" трения. Как мы выяснили, при малых скоростях сопротивление зависит от вязкости жидкости, скорости движения и линейных размеров тела. Рассмотрим теперь законы трения при больших скоростях. Но прежде надо сказать, какие скорости считать малыми, а какие большими. Нас интересует не абсолютная величина скорости, а то8 является ли скорость достаточно малой, чтобы выполнялся рассмотренный выше закон вязкого трения.

Оказывается, нельзя назвать такое число метров в секунду, чтобы во всех случаях при меньших скоростях были, применимы законы вязкого трения. Граница применения изученного нами закона зависит от размеров тела и от степени вязкости и плотности жидкости.

Для воздуха "малыми" являются, скорости меньше

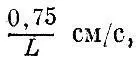
для воды - меньше

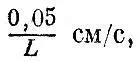
а для вязких жидкостей, вроде густого меда, - меньше

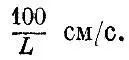
Таким образом, к воздуху и особенно к воде законы вязкого трения мало применимы: даже при малых скоростях, порядка 1 см/ с, они будут годиться лишь для крошечных тел миллиметрового размера. Сопротивление, испытываемое ныряющим в воду человеком, ни в какой степени не подчиняется закону вязкого трения.

Чем же объяснить, что при изменении скорости меняется закон сопротивления среды? Причины надо искать в изменении характера обтекания жидкостью движущегося в нем тела. На рис. 6.3 изображены два круговых цилиндра, движущихся в жидкости (ось цилиндра перпендикулярна к чертежу). При медленном движении жидкость плавно обтекает движущийся предмет - сила сопротивления, которую ему приходится преодолевать, есть сила вязкого трения (рис. 6.3, а). При большой скорости позади движущегося тела возникает сложное запутанное движение жидкости (рис. 6.3, б). В жидкости то появляются, то пропадают различные струйки, они образуют причудливы фигуры, кольца, вихри. Карта на струек все время меняется. Появление этого движения, называемого турбулентным, в корне меняет закон сопротивления.

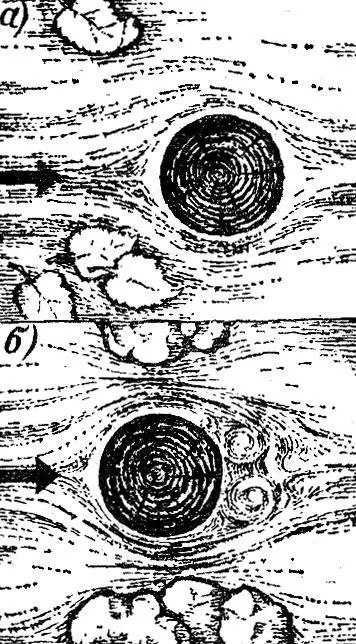
Рис. 6.3

Турбулентное сопротивление зависит от скорости и размеров предмета совсем иначе, чем вязкое: оно пропорционально квадрату скорости и квадрату линейных размеров. Вязкость жидкости при этом движении перестает играть существенную роль; определяющим свойством становится ее плотность,- причем сила сопротивления пропорциональна первой степени плотности жидкости (газа). Таким образом, для силы F турбулентного сопротивления справедлива формула .

F ~ ρν2L2,

где ν - скорость движения, L - линейные размеры предмета и ρ - плотность среды. Числовой коэффициент пропорциональности, который мы не написали, имеет различные значения в зависимости от формы тела.

Движение в воздухе, как мы говорили выше, почти всегда "быстрое", т. е. основную роль играет турбулентное, а не вязкое сопротивление. Турбулентное сопротивление испытывают самолеты, птицы, парашютисты. Если человек падает в воздухе без парашюта, то через некоторое время он начинает падать равномерно (сила сопротивления уравновешивает вес), но с весьма значительной скоростью, порядка 50 м/ с. Раскрывание парашюта приводит к резкому замедлению падения - тот же вес уравновешивается теперь сопротивлением купола парашюта. Так как сила сопротивления пропорциональна скорости движения и размеру падающего, предмета в одинаковой степени, то скорость упадет во столько раз, во сколько изменятся линейные размеры падающего тела. Диаметр парашюта около 7 м, "диаметр" человека около одного метра. Скорость падения уменьшается до 7 м/ с. С такой скоростью можно безопасно приземлиться.

Надо сказать, что задача увеличения сопротивления решается значительно легче, чем обратная задача. Уменьшить сопротивление автомобилю и самолету со стороны воздуха или подводной лодке со стороны воды - важнейшие и нелегкие технические задачи.

Оказывается, что, изменяя форму тела, можно уменьшить турбулентное сопротивление во много раз. Для этого надо свести к минимум турбулентное движение, являющееся источником сопротивления. Это достигается приданием предмету специальной, как говорят, обтекаемой формы.