Закон Авогадро указывает, что при определенных давлении и температуре отношение числа молекул к объему, в котором они заключены, N/ V, есть величина, одинаковая для всех газов.
Так как плотность газа ρ = Nm/ V, то отношение плотностей газов равно отношению их молекулярных масс:
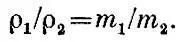
Относительные массы молекул могут быть поэтому установлены простым взвешиванием газообразных веществ. Такие измерения сыграли в свое время большую роль в развитии химии. Из закона Авогадро следует также, что для моля любого вещества, находящегося в состоянии идеального газа, ρV = k N AT, где к - универсальная постоянная (она носит имя замечательного немецкого физика Людвига Больцмана), равная 1,38.10 -16эрг/ К. Произведение R= k N Aназывают универсальной газовой постоянной.
Закон идеального газа записывают часто как
ρV = μRT,
где μ - количество вещества, выраженное в молях. Это уравнение часто используется на практике.
Теория указывает, что при одной температуре средние кинетические энергии молекул m v 2 ср/2 одинаковы. При нашем определении температуры эта средняя кинетическая энергия поступательного движения молекул газа пропорциональна абсолютной температуре. Комбинируя уравнение идеального газа и уравнение Бернулли, найдем
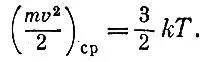
Измерение температуры термометром, заполненным идеальным газом, придает этой мере простой смысл: температура пропорциональна среднему значению энергии поступательного движения молекул. Поскольку мы живем в трехмерном пространстве, про точку, движущуюся как угодно, можно сказать: она имеет три степени свободы. Значит, на одну степень свободы движущейся частицы приходится кТ/ 2энергии.
Определим среднюю скорость молекул кислорода при комнатной температуре, которую мы для круглого счета примем в 27°С=300 К. Масса одной молекулы кислорода равна 32/ (6*10 23 ). Простое вычисление даст м ср= 4,8*10 4см/с, т.е. около 500 м/с. Существенно быстрее движутся молекулы водорода. Их массы в 16 раз меньше и скорости в 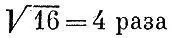 больше, т. е. при комнатной температуре составляют около 2 км/с. Прикинем, с какой тепловой скоростью движется маленькая? видимая в микроскоп частичка. Обычный микроскоп позволяет увидеть пылинку диаметром в 1 мкм (10 -4см). Масса такой частицы при плотности,; близкой к единице, будет что-нибудь около 5*10 -13г. Для ее скорости получим около 0,5 см/с. Неудивительно, что такое движение вполне заметно.
больше, т. е. при комнатной температуре составляют около 2 км/с. Прикинем, с какой тепловой скоростью движется маленькая? видимая в микроскоп частичка. Обычный микроскоп позволяет увидеть пылинку диаметром в 1 мкм (10 -4см). Масса такой частицы при плотности,; близкой к единице, будет что-нибудь около 5*10 -13г. Для ее скорости получим около 0,5 см/с. Неудивительно, что такое движение вполне заметно.
Скорость броуновского движения горошины с массой в 0,1 г будет уже всего только 10 -6см/с. Немудрено, что мы не видим броуновского движения таких частиц.
Мы говорим о средних скоростях молекулы. Но ведь не все молекулы движутся с одинаковыми скоростями, какая-то доля молекул движется быстрее, а какая-то медленнее. Все это, оказывается можно рассчитать. Приведем только результаты.
При температуре около 15°С, например, средняя скорость молекул азота равна 500 м/с, со скоростями от 300 до 700 м/с движется 59% молекул. С малыми скоростями - от 0 до 100 м/с - движется всего лишь 0,6% молекул. Быстрых молекул со скоростями свыше 1000 м/с в газе всего лишь 5,4% (см. рис. 3.2).
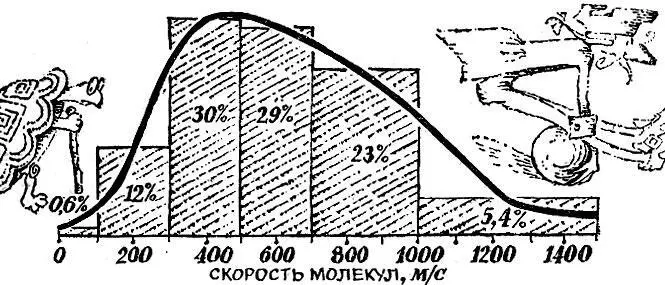
Рис. 3.2
Основание каждого столбика рисунка построено на интервале скоростей, о котором идет речь, а площадь пропорциональна доле молекул, скорости которых лежат в этом интервале.
Можно рассчитать и распределение молекул по разным значениям энергии поступательного движения-
Число молекул энергия которых более чем в два раза превосходит среднюю, уже меньше 10%. Доля еще более "энергичных" молекул тает по мере увеличения энергии во все возрастающей степени. Так, молекул, энергия которых в 4 раза больше средней,- всего 0,7%, в 8 раз больше средней - 0,06*10 -4%, в 16 раз больше средней - 2*10 -8%.
Энергия молекулы кислорода, движущейся со скоростью 11 км/ с, равна 23*10 -12эрг. Средняя энергия молекулы при комнатной температуре равна всего 6*10 -14эрг. Таким образом, энергия "одиннадцати-километрозой молекулы" по крайней мере в 500 раз больше энергии молекулы со средней скоростью. Неудивительно, что доля молекул со скоростями выше 11 км/ сравна невообразимо малому числу - порядка 10 -300.
Читать дальше

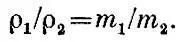
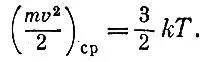
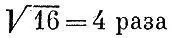 больше, т. е. при комнатной температуре составляют около 2 км/с. Прикинем, с какой тепловой скоростью движется маленькая? видимая в микроскоп частичка. Обычный микроскоп позволяет увидеть пылинку диаметром в 1 мкм (10 -4см). Масса такой частицы при плотности,; близкой к единице, будет что-нибудь около 5*10 -13г. Для ее скорости получим около 0,5 см/с. Неудивительно, что такое движение вполне заметно.
больше, т. е. при комнатной температуре составляют около 2 км/с. Прикинем, с какой тепловой скоростью движется маленькая? видимая в микроскоп частичка. Обычный микроскоп позволяет увидеть пылинку диаметром в 1 мкм (10 -4см). Масса такой частицы при плотности,; близкой к единице, будет что-нибудь около 5*10 -13г. Для ее скорости получим около 0,5 см/с. Неудивительно, что такое движение вполне заметно.