Амит Госвами - Самосознающая вселенная. Как сознание создает материальный мир

Теперь становится очевидным случай соотношения неравенства, описанного Беллом. Начнем с параллельным расположением детекторов; теперь наблюдаемые последовательности идентичны. Изменим установку детектора Мо на угол А (рис. 31, б), и последовательности перестают быть одинаковыми; теперь они содержат ошибки — в среднем одну ошибку на каждые четыре наблюдения. Аналогичным образом, вернемся к параллельной установке детекторов, и на этот раз изменим установку детектора Джо на тот же угол А (рис. 31, в); снова будет в среднем одна ошибка на каждые четыре наблюдения. Этот результат не зависит от того, как далеко друг от друга находятся детекторы и их наблюдатели. Один может быть в Нью-Йорке, другой в Лос-Анджелесе, а источник фотонов — где-то посередине.

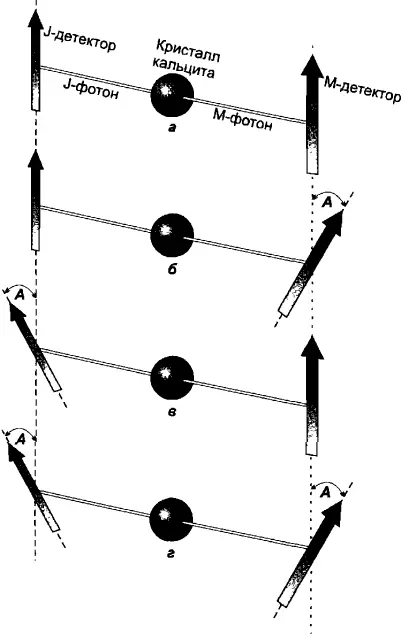
Рис. 31. Как возникает неравенство Белла. Если бы скрытые переменные были локальными, то частота появления ошибок (отклонение от полной корреляции) в экспериментальной обстановке (г) была бы равна, самое большее, сумме частот появления ошибок в двух обстановках (б) и (в)

Если локальность справедлива, если постулируемые скрытые переменные, которые заставляют фотоны принимать определенные направления поляризации, требуемые ситуацией, локальны, то мы можем с полной уверенностью говорить: что бы вы ни делали с детектором Джо, это не может изменять сообщение Мо — во всяком случае, не мгновенно. И наоборот. Таким образом, если, начав с параллельных установок, наблюдатель Джо поворачивает детектор Джо на угол А и если наблюдатель Мо одновременно поворачивает детектор Мо на тот же угол в противоположную сторону (так что детекторы теперь расположены под углом 2А друг к другу, рис. 32, г), то какова должна быть частота появления ошибок? Если справедливо предположение локальности скрытых переменных, то действие каждого наблюдателя приводит, в среднем, к одной ошибке на четыре наблюдения, так что суммарная частота появления ошибок составит 2 на четыре наблюдения. Однако может случиться, что ошибка Джо время от времени погашает ошибку Мо. Таким образом, частота появления ошибок будет меньшей или равной 2/4 — это и есть неравенство Белла. Однако квантовая механика предсказывает частоту появления ошибок 3/4. (Доказательство этого выходит за рамки данной книги.) Итак, теорема Белла гласит: теория локальных скрытых переменных несовместима с квантовой механикой.

Неравенства Белла подвергались экспериментальному исследованию. В 1972 г. физики из Университета Беркли Джон Клаузер и Стюарт Фридман показали, что неравенства Белла действительно нарушаются, и квантовая механика реабилитирована. Затем Аспект своим экспериментом доказал, что между двумя детекторами вообще не может быть никаких локальных сигналов.

Заметьте, что работа Белла (а также работа Бома, поскольку она привела к идее измерения поляризационной корреляции) подготовила почву для эксперимента Аспекта, утвердившего нелокальность в квантовой механике. Теперь вы можете оценить, почему на конференции по физике в 1985 г. группа физиков пела на мотив «Колокольчики звенят» («Jingle Bells») такие слова:

Согласно теореме Белла и эксперименту Аспекта, если скрытые переменные существуют, они должны быть способны мгновенно воздействовать на скоррелированные квантовые объекты, даже если они находятся в разных концах галактики. Когда в эксперименте Аспекта один экспериментатор изменяет настройку своего детектора, скрытые переменные управляют не только фотоном, достигающим этого детектора, но и его далеким партнером. Скрытые переменные способны действовать нелокально. Теорема Белла разрушает догму локальных причины и следствия, принятую в классической физике. Даже если вводить скрытые переменные, чтобы найти причинную интерпретацию квантовой механики, как это делает Дэвид Бом, эти скрытые переменные должны быть нелокальными.

Дэвид Бом сравнивает эксперимент Аспекта с видением рыбки на двух разных экранах двух телевизоров. Что бы ни делала одна рыбка, делает и другая. Если считать изображения рыбки первичной реальностью, это кажется странным, но с точки зрения «реальной» рыбки, все очень просто.