На обеих станциях имеются часы. На первой станции в вагон садится путешественник и перед отходом поезда проверяет свои часы по станционным. По приезде на другую станцию он с удивлением замечает, что его часы отстали. В мастерской путешественника заверили, что его часы в полном порядке.
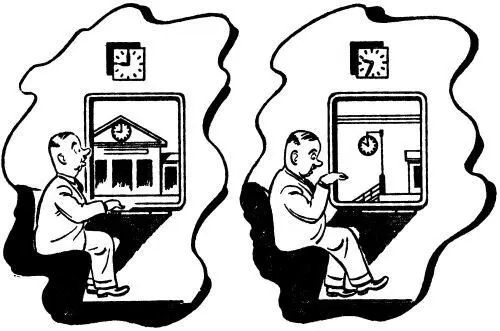
В чем же дело?
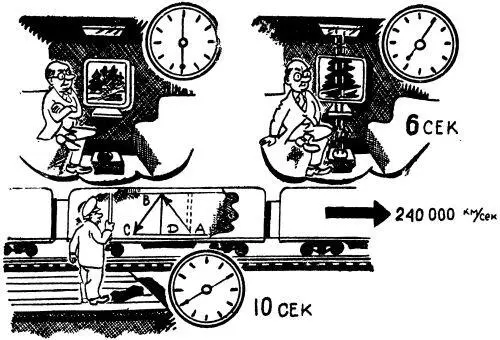
Чтобы разобраться в этом, представим, что пассажир направляет к потолку луч света из фонарика, поставленного на пол вагона. На потолке расположено зеркало, от которого луч света отражается обратно к лампочке фонарика. Путь луча, каким его видит пассажир в вагоне, изображен в верхней части рисунка на стр. 51. Совсем иначе выглядит этот путь для наблюдателя, находящегося на платформе. За то время, что луч света пройдет от лампочки до зеркала, само зеркало вследствие движения поезда переместится. Пока луч будет возвращаться, лампочка переместится еще на такое же расстояние.
Мы видим, что для наблюдателей на платформе свет прошел явно большее расстояние, чем для наблюдателей в поезде. С другой стороны, мы знаем, что скорость света есть абсолютная скорость, она одинакова и для едущих в поезде, и для тех, кто стоит на платформе. Это заставляет нас сделать вывод: на станции между отправлением и возвращением луча света прошло больше времени, чем в поезде!
Нетрудно вычислить отношение времен.
Предположим, наблюдатель на платформе установил, что между отправлением и возвращением луча света прошло 10 секунд. За эти 10 секунд свет пробежал 300 000 X 10 = 3 000 000 километров. Отсюда следует, что стороны АВ и ВС равнобедренного треугольника ABC составляют каждая 1 500 000 километров. Сторона АС равна, очевидно, пути, пройденному поездом за 10 секунд, то есть 240 000 X 10 = 2 400 000 километров.
Теперь легко определить высоту вагона, которая будет высотой BD треугольника ABC.
В прямоугольном треугольнике квадрат гипотенузы (АВ) равен сумме квадратов катетов (AD и BD). Из равенства: AB 2= AD 2+ BD 2получаем, что высота вагона 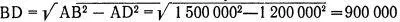 километров. Высота весьма солидная, что, впрочем, не удивительно при астрономических размерах поезда Эйнштейна.
километров. Высота весьма солидная, что, впрочем, не удивительно при астрономических размерах поезда Эйнштейна.
Путь, пройденный лучом от пола до потолка вагона и обратно, с точки зрения пассажира, равен, очевидно, удвоенной высоте, то есть 2 X 900 000 = 1 800 000 километров. Для прохождения этого пути свету понадобится 1 800 000 / 300 000 = 6 секунд.
Часы систематически отстают
Итак, в то время как на станции прошло 10 секунд, в поезде — всего лишь 6 секунд. Значит, если по станционному времени поезд пришел через час после своего отправления, то по часам пассажира пройдет всего 60 X (6 / 10) = 36 минут. Другими словами, часы путешественника отстали от станционных за час на 24 минуты.
Нетрудно догадаться, что отставание часов будет тем значительнее, чем больше скорость поезда.
Действительно, чем ближе скорость поезда к скорости света, тем ближе катет AD, изображающий путь, пройденный поездом, к гипотенузе АВ, изображающей путь, пройденный за то же время светом. Соответственно этому уменьшается отношение катета BD к гипотенузе. Но это отношение и представляет собой отношение времени в поезде и на станции. Приближая скорость поезда к скорости света, мы сможем добиться, чтобы за час станционного времени в поезде прошел сколь угодно малый промежуток времени. Так, при скорости поезда, равной 0,9999 скорости света, за час станционного времени в поезде пройдет лишь одна минута!
Таким образом, всякие движущиеся часы отстают от покоящихся. Не противоречит ли этот результат принципу относительности движения, из которого мы исходили?
Не означает ли это, что те часы, которые идут быстрее всех других, находятся в абсолютном покое?
Нет, потому что сравнение часов в поезде с часами на станциях происходило в совершенно неравноценных условиях. Ведь было не двое, а трое часов! Свои часы путешественник сравнивал с двумя разными часами на разных станциях. И наоборот, если бы в переднем и заднем вагонах поезда были вывешены часы, то наблюдатель на одной из станций, сравнивая показания станционных часов с показаниями часов в окнах проносящегося мимо него поезда, обнаружил бы, что систематически отстают станционные часы.
Читать дальше



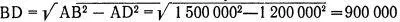 километров. Высота весьма солидная, что, впрочем, не удивительно при астрономических размерах поезда Эйнштейна.
километров. Высота весьма солидная, что, впрочем, не удивительно при астрономических размерах поезда Эйнштейна.




![Лев Балашов - Занимательная философия. Учебное пособие [6-е издание, переработанное и дополненное]](/books/388554/lev-balashov-zanimatelnaya-filosofiya-uchebnoe-posobie-6-e-izdanie-pererabotannoe-i-dopolnennoe-thumb.webp)





