Задание 1-формы в данной точке (связь с точечным описанием) для некоторого геометрического объекта, описывающего физическую величину, например, для тензора произвольного ранга (0-ранг — скаляр, 1-ранг — вектор или 1-форма, 2-ранг — тензор второго ранга и т. д.), предполагает выполнение трех основных операций. Это, прежде всего, задание вектора смещения, в направлении которого данный объект меняется от точки к точке. Во-вторых: моделирование исходного объекта в окрестностях каждой точки в виде плоских поверхностей уровня, расположенных на одинаковых расстояниях. Инаконец, подсчет числа пересечений этих плоскостей вектором смещения. Поскольку образование 1-формы (градиента) от произвольного тензора предполагает одновременное задание вектора смещения, появляется дополнительный входной канал, и ранг исходного тензора увеличивается на единицу.
Таким образом, дифференциальная геометрия дает более строгое определение градиента в качестве 1-формы, в отличие от обычных представлений градиента как вектора. Градиент, который нам более знаком, — это всего лишь вектор, поставленный в соответствие 1-форме градиента с помощью уравнения (которое уже приводилось) 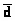 f · v= á d f , vñ, где слева стоит скалярное произведение двух векторов, и
f · v= á d f , vñ, где слева стоит скалярное произведение двух векторов, и 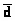 f — градиент в виде вектора.
f — градиент в виде вектора.
Дифференциальная геометрия расширяет также понятие тензора. Если обычно под тензором понимается линейный оператор с входными каналами для векторов и выходными данными либо в виде вещественных чисел, либо в виде векторов, то теперь во входной канал может подаваться не только вектор, но и 1-форма.
В качестве примера рассмотрим координатное представление тензора второго ранга. В отличие от обычного вектора, который может быть разложен лишь в одном произвольном базисе из ортонормированных векторов (поэтому его можно считать тензором первого ранга), тензор второго ранга разлагается на компоненты в двух базисах. В качестве любого из этих базисов (или обоих сразу) могут служить либо наборы из обычных базисных векторов e α, либо совокупность так называемых базисных 1-форм w α= d x α. Базисные 1-формы — это координатные поверхности x α = const. Следовательно, базисный вектор e αпересекает только одну поверхность базисной1-формы w α(перпендикулярную e α).
Точно так же, как произвольный вектор можно разложить по базису e α, v= ν α e α, произвольную1-форму можно разложить по базису w β, σ = σ β w β. Коэффициенты ν αи σ βназываются компонентами вектора vи 1-формы s в базисе e αи w βсоответственно.
Вводя в некоторый тензор второго ранга Sпроизвольные вектор vи 1-форму σ и, зная компоненты их разложения в своих базисах, через них можно выразить компоненты самого тензора S( v, σ) = S( e α, w β) v ασ β= S α β v ασ β.
Вектор состояния — полное описание замкнутой системы в выбранном базисе. Задается лучом гильбертова пространства.
Волновая функция (волновой вектор) — частный случай вектора состояния, одно из координатных его представлений, когда в качестве базиса выбираются пространственно-временные координаты.
Гильбертово пространство (пространство состояний) — совокупность всех потенциально возможных состояний системы.
Декогеренция — физический процесс, при котором нарушается нелокальность и уменьшается квантовая запутанность между составными частями системы в результате ее взаимодействия с окружением. При этом подсистемы «проявляются» из нелокального состояния в виде отдельных самостоятельных элементов реальности, они обосабливаются, отделяются друг от друга, приобретая видимые локальные формы.
Запутанность — см . несепарабельность.
Интерференция — одно из наиболее широко известных проявлений суперпозиции состояний (например, в оптике). Интерференцией света в тонких пленках объясняется, например, радужная окраска мыльных пузырей и масляных пленок. Интерференция имеет место только для когерентных состояний. Декогеренцию (нарушение когерентности) в этом случае можно рассматривать как подавление интерференции. Каждая частица (например, фотон) интерферирует лишь сама с собой. Интерференции между двумя разными фотонами никогда не происходит, точнее, реализовать эту ситуацию на практике (экспериментально) очень сложно.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

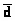 f · v= á d f , vñ, где слева стоит скалярное произведение двух векторов, и
f · v= á d f , vñ, где слева стоит скалярное произведение двух векторов, и 



![Сергей Куц - Тёмная магия [litres]](/books/393901/sergej-kuc-temnaya-magiya-litres-thumb.webp)
![Сергей Лукьяненко - Время для мага. Лучшая фантастика 2020 [сборник litres]](/books/406050/sergej-lukyanenko-vremya-dlya-maga-luchshaya-fantastik-thumb.webp)





