Брайан Грин - Скрытая реальность. Параллельные миры и глубинные законы космоса

Другой подход к задаче полного определения теории струн, возникший из более ранних работ в этой области, называется Матричной теорией (что даёт ещё одно возможное объяснение для значения буквы «M» в M-теории). Этот подход был разработан Томом Бэнксом, Вили Фишлером, Стивом Шенкером и Леонардом Сасскиндом.

Я указал число 10 55грамм, что соответствует содержимому наблюдаемой вселенной на современном этапе, но в более ранние времена температура содержимого вселенной была выше, и поэтому оно имело бо́льшую энергию. Поэтому 10 65грамм является более точной оценкой для той массы, которую вам потребуется собрать в крохотное зёрнышко для повторения эволюции нашей Вселенной с того момента, когда её возраст составлял примерно одну секунду.

Можно подумать, что поскольку ваша скорость ограничена сверху скоростью света, то ваша кинетическая энергия также будет ограничена. Но это не так. По мере того как ваша скорость приближается к скорости света, ваша энергия увеличивается; из специальной теории относительности следует, что она не ограничена. Математически формула вашей энергии имеет вид:

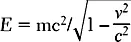
где c — это скорость света, а υ — ваша скорость. Как можно видеть, когда υ стремится к c , энергия E неограниченно растёт. Отметим также, что это справедливо с точки зрения наблюдателя, который следит за вашим падением, например, кого-то, неподвижно стоящего на поверхности Земли. С вашей точки зрения, пока вы свободно падаете, вы неподвижны, а окружающая вас материя постоянно набирает скорость.

На нашем текущем уровне понимания имеется значительный разброс в таких оценках. Величина в 10 грамм возникает из следующих рассуждений: считается, что энергетический масштаб инфляции составляет примерно 10 −5от планковской энергии, которая превышает примерно в 10 19энергию, эквивалентную массе протона. (Если бы инфляция происходила на бо́льших масштабах энергии, то по некоторым оценкам мы уже должны были бы наблюдать гравитационные волны, порождённые в ранней вселенной.) В более привычных единицах планковский масштаб составляет примерно 10 −5грамма (небольшая величина по обычным меркам, но на масштабе физики элементарных частиц, где говорится об энергии, переносимой отдельными частицами, она огромна). Таким образом, плотность энергии поля инфлатона будет составлять примерно 10 −5грамма на каждую кубическую единицу объёма, линейный размер которого определяется расстоянием, кратным планковской длине с множителем 10 5(напомним, что из соотношения квантовой неопределённости следует, что энергия и длина обратно пропорциональны друг другу), что составляет примерно 10 −28сантиметра. Таким образом, полная масса-энергия поля инфлатона в объёме с ребром в 10 −26сантиметра равна 10 −5грамма/(10 −28сантиметра) 3× (10 −26сантиметра) 3, что составляет примерно 10 грамм. Те, кто прочитал «Ткань космоса», возможно помнят, что там я использовал несколько иное значение. Различие возникло из предположения, что энергетический масштаб инфлатона был несколько выше.

Hans Moravec, «Robot: Mere Machine to Transcendent Mind». New York: Oxford University Press, 2000. См. также: Ray Kurzweil, «The Singularity Is Near: When Humans Transcend Biology». New York: Penguin, 2006.

См., например: Robin Hanson, «How to Live in a Simulation», «Journal of Evolution and Technology» 7, 1 (2001).

Согласно тезису Чёрча — Тьюринга, любой компьютер так называемого универсального тьюрингова типа может моделировать действия другого компьютера, поэтому вполне справедливо, что находящийся внутри симуляции компьютер — он сам смоделирован основным компьютером, на котором выполняется общая симуляция — может решать определённые задачи, эквивалентные тем, что решаются на основном компьютере.

Философ Дэвид Льюис развил похожую идею, названную им модальным реализмом. См.: Lewis David, «On the Plurality of Worlds». Malden, Mass.: Wiley-Blackwell, 2001. Однако, мотивация Льюиса для введения всех возможных вселенных отличается от мотивации Нозика. Льюису нужен был контекст, в котором, например, могли бы воплотиться нереализованные утверждения (такие как «если бы Гитлер выиграл войну, то мир был бы другим»).

Джон Барроу высказывал похожее мнение в: John Barrow, «Pi in the Sky». New York: Little, Brown, 1992.

При более детальном обсуждении вычислимых и невычислимых функций мы встретимся с функциями, вычислимыми с любой наперёд заданной точностью . Это функции, для которых имеется конечный алгоритм вычисления значений с растущей точностью. Например, это имеет место для вычисления числа π с точностью до определённого количества знаков: компьютер может вычислить в π каждый последующий знак после запятой, хотя никогда не достигнет конца вычислений. Поэтому, хотя π , строго говоря, не является вычислимым числом, оно вычислимо с любой наперёд заданной точностью. Однако большинство вещественных чисел непохожи на π . Они не просто невычислимы, они также невычислимы с любой наперёд заданной точностью.