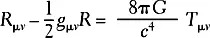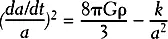Брайан Грин - Скрытая реальность. Параллельные миры и глубинные законы космоса

Этот закон определяет силу гравитационного притяжения F между двумя объектами с заданными массами m 1и m 2и расстоянием r между ними. Математически закон имеет вид F = Gm 1 m 2/ r 2, где G обозначает константу Ньютона — экспериментально измеренное число, характеризующее силу гравитационного взаимодействия.

Для математически подкованного читателя приведём уравнения Эйнштейна:

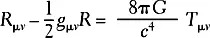
где g — это метрика пространства-времени, R μν — тензор кривизны Риччи, R — скалярная кривизна, G — константа Ньютона, T μν — тензор энергии-импульса.

За десятилетия, прошедшие с момента этого знаменитого подтверждения общей теории относительности, возникли вопросы, касающиеся надёжности полученных результатов. Чтобы увидеть световой луч от удалённой звезды, огибающий Солнце, наблюдения должны были проводиться во время солнечного затмения; к сожалению, плохая погода затруднила получение чётких фотографий затмения 1919 года. Вопрос в том, могли ли Эддингтон и его сотрудники внести систематическую ошибку под влиянием ожидаемого результата: отбраковывая фотографии, кажущиеся ненадёжными по причине интерференции, вызванной погодными условиями, они могли бы исключить несоразмерное количество фотографий с данными, которые казались противоречащими теории Эйнштейна. Недавнее подробное исследование Даниэля Кеннефика (см.: www.arxiv.org, paper arXiv:0709.0685, в котором, помимо прочих рассмотрений, делается современная переоценка фотографических пластинок, сделанных в 1919 году) убедительно свидетельствует что подтверждение теории, сделанное в 1919 году, на самом деле является надёжным.

Для заинтересованного читателя приведём уравнения Эйнштейна общей теории относительности, которые в рассматриваемом случае выглядят так:

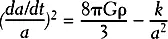
Переменная a ( t ) является масштабным фактором вселенной — её значение, как указывает название, устанавливает масштаб расстояния между объектами (если значения a ( t ) в два разных момента времени отличаются, например, в 2 раза, то расстояние между двумя частными галактиками будет отличаться между этими временами также в 2 раза), G — это константа Ньютона, ρ — плотность материи/энергии, и k является параметром, значение которого может быть 1, 0 или −1, в зависимости от того, является ли форма пространства сферической, евклидовой («плоской») или гиперболической. Обычно считается, что вид этого уравнения был найден Александром Фридманом и, собственно, называется уравнением Фридмана.

Внимательный читатель может отметить два момента. Во-первых, в общей теории относительности, как правило, мы определяем координаты, которые сами зависят от находящегося в пространстве вещества: мы используем галактики в качестве носителей координат (как будто на каждой галактике «нарисован» частный набор координат — так называемые движущиеся системы координат). Поэтому для задания определённой области пространства обычно ссылаются на присутствующую в ней материю. Тогда более точная перефразировка текста такова: область пространства, в которой находится некоторая группа из N галактик в момент времени t 1, будет иметь больший объём в более поздний момент времени t 2. Во-вторых, интуитивно понятное утверждение, касающееся плотности материи и энергии, изменяющиеся при расширении или сжатии пространства, содержит неявное предположение насчёт уравнения состояния материи и энергии. Есть ситуации и скоро мы столкнёмся с одной из них, когда пространство может расширяться или сжиматься, а плотность некоторого вклада энергии — плотность энергии так называемой космологической постоянной — остаётся неизменной. Действительно, есть даже более экзотические сценарии, в которых пространство расширяется а плотность энергии при этом растёт . Такое происходит, потому что при определённых обстоятельствах гравитация служит источником энергии. Важный момент этого параграфа состоит в том, что уравнения общей теории относительности в исходном виде противоречат статичной вселенной.

Двумерный тор обычно изображается как пустой бублик. Двухшаговый процесс показывает, что эта картинка согласована с приведённым в тексте книги описанием. Когда, достигнув правого края экрана, вы попадаете назад на левый край, это равносильно отождествлению всего правого края с левым краем. Если бы экран был гибким (например, из тонкого пластика), то такое отождествление могло бы быть буквальным, если скатать экран в цилиндр и объединить вместе правый и левый края. Когда, ступив на верхний край, вы попадаете в нижний, то это тоже равносильно отождествлению этих краёв. Это достигается явным образом на втором шаге, в котором мы скручиваем цилиндр и соединяем верхний и нижний круговые края. Получившаяся фигура выглядит как обычный бублик. Обманчивый аспект этих манипуляций состоит в том, что поверхность бублика выглядит искривлённой; если его поверхность покрыть отражающей краской, то ваше отражение будет искажено. Это артефакт реализации тора в виде объекта, расположенного в объемлющем трёхмерном пространстве. В действительности, являясь двумерной поверхностью, тор не искривлён. Он плоский. Что очевидно, если его представить в виде плоского экрана для видеоигр. Именно поэтому в тексте книги я выбрал более фундаментальное описание в виде фигуры, края которой попарно отождествляются.