Брайан Грин - Элегантная вселенная (суперструны, скрытые размерности и поиски окончательной теории)

Примерно за десятилетие Эйнштейн в одиночку сокрушил многовековые устои теории Ньютона, представив миру совершенно новую и значительно более глубокую теорию гравитации. И эксперты, и неспециалисты были покорены завораживающим изяществом и фундаментальной новизной формулировки общей теории относительности Эйнштейна. Не следует, однако, забывать о благоприятных исторических обстоятельствах, в значительной мере способствовавших успеху исследований Эйнштейна. Главное из них состоит в том, что Эйнштейну были известны математические результаты, полученные в XIX в. Георгом Бернгардом Риманом. Эти результаты давали возможность описания искривленных пространств произвольной размерности в рамках строгого геометрического аппарата. В знаменитой инаугурационной лекции 1854 г. в Геттингенском университете Риман перешел через Рубикон мышления в рамках плоского евклидового пространства и проложил дорогу к единообразному математическому описанию геометрии всех типов искривленных пространств. Именно пионерские идеи Римана позволили математикам дать количественное описание искривленных пространств, подобных тем, которые иллюстрировались на рис. 3.4 и 3.6. Гениальность Эйнштейна состояла в осознании того, что эти математические идеи были идеально приспособлены для выражения его новых взглядов на гравитационное взаимодействие. Он смело заявил о том, что математические понятия римановой геометрии безупречно согласуются с физикой гравитации.

Но сейчас, почти век спустя после научного подвига Эйнштейна, теория струн дает нам квантово-механическое описание гравитации, требующее пересмотра общей теории относительности на длинах порядка планковской. А так как в основе общей теории относительности лежит понятие римановой геометрии, то и само это понятие должно быть модифицировано для соответствия новой физике, возникающей на малых расстояниях в теории струн. И если в общей теории относительности постулируется, что свойства искривленного пространства Вселенной описываются геометрией Римана, то в теории струн утверждается, что данный постулат справедлив лишь в случае, когда структура Вселенной рассматривается на достаточно больших масштабах. На длинах порядка планковской должна вступать в игру новая геометрия, согласующаяся с новой физикой теории струн. Эту новую геометрию называют квантовой геометрией.

В отличие от геометрии Римана, здесь нет готовых геометрических рецептов, уже описанных в книгах по математике и пригодных для того, чтобы занимающиеся струнами физики могли взять их на вооружение и использовать в этой науке. Напротив, современные физики и математики погружены в исследования в теории струн, по крупицам собирая знания, которые лягут в основу новой области физики и математики. И хотя основная часть работы еще впереди, в ходе этих исследований уже было открыто много новых диктуемых теорией струн геометрических свойств пространства-времени, которые наверняка произвели бы впечатление и на самого Эйнштейна.

При прыжках на батуте его упругие волокна растягиваются под весом человеческого тела, и батут деформируется. Сильнее всего растяжение вблизи тела человека, а по мере приближения к краям батута растяжение менее заметно. Это наглядно видно, если на батут нанесено знакомое изображение (например, Мона Лиза). Если на батуте никто не стоит, изображение выглядит нормально, но если на батут встает человек, изображение искажается, в особенности непосредственно под человеком (см. рис. 10.1).

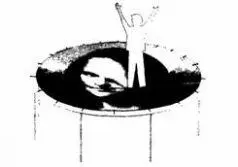
Рис. 10.1. Если на батуте с нанесенным изображением стоит человек, изображение сильнее всего искажается под весом тела человека.

Этот пример иллюстрирует важнейший принцип описания искривленных поверхностей, принятый в математической формулировке Римана. На основе более ранних наблюдений Карла Фридриха Гаусса, Николая Лобачевского, Яноша Бойяи и других математиков, Риман показал, что детальный анализ расстояний между всеми точками на поверхности объекта или внутри него дает способ вычисления значения кривизны. Грубо говоря, чем больше (неоднородное) растяжение, тем сильнее отклонение от формулы для расстояний в плоском случае, и тем больше кривизна объекта. Например, батут сильнее всего растягивается под ногами человека, и поэтому расстояния между точками в этой области будут сильнее всего отличаться от расстояний в случае ненагруженного батута. Следовательно, кривизна батута здесь будет максимальной. Это интуитивно ясно из приведенного рисунка: именно в таких точках изображение на батуте искажено сильнее всего.