Дэйв Голдберг - Вселенная в зеркале заднего вида. Был ли Бог правшой? Или скрытая симметрия, антивещество и бозон Хиггса

Ньютон, как и Кеплер, обнаружил, что все планеты теоретически должны вращаться вокруг Солнца по идеальным эллипсам. Однако с Меркурием что-то не заладилось: его перигелий смещается примерно на 2 градуса в столетие. На практике это означает, что орбита Меркурия — не идеальный эллипс, а узор в виде розетки. Этот эффект почти целиком объясняется простым ньютоновым воздействием остальных планет, особенно Юпитера. Однако небольшая доля смещения, примерно 43 угловые секунды в сто лет, в рамках теории Ньютона объяснить невозможно. Прецессию Меркурия можно как-то истолковать лишь в том случае, если вы понимаете, что пространство-время вблизи Солнца искажается.

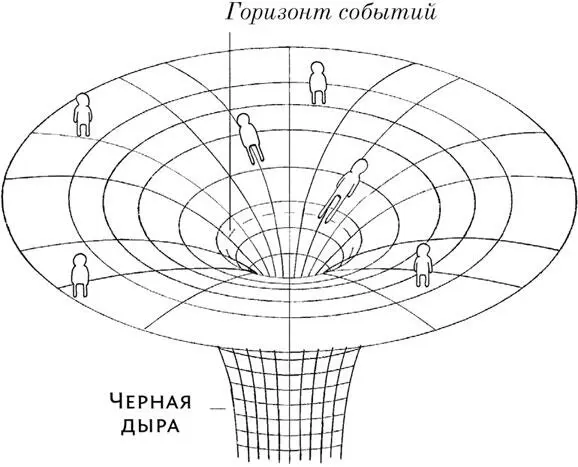
Если бы Солнце было черной дырой, мы могли бы подобраться гораздо ближе, и воздействие гравитации было бы гораздо зрелищнее. Как мы уже видели, рядом с массивными телами время течет медленнее, чем вдали от них. На горизонте событий черной дыры замедление времени становится буквально бесконечным. Да-да, вы не ослышались: бесконечным.

Предположим, у вас есть приятельница, которой вы не прочь пожертвовать ради науки. Давайте возьмем Алису: похоже, она не питает отвращения к кроличьим норам и всему такому прочему. Возьмите веревку попрочнее и подвесьте Алису над самым горизонтом событий. С точки зрения Алисы пройдет всего несколько минут, но к тому моменту, как она взберется обратно, в остальной вселенной, вероятно, пройдут тысячи лет. Не исключено, что к этому времени Землей будут править немытые обезьяны!

Спагеттификация

А теперь предположим, что Алиса решила не ждать, когда вы плавно спустите ее, а пожертвовать собой и прыгнуть в черную дыру «солдатиком». Разъясню еще раз: я не предлагаю ни вам, ни вашим друзьям подходить к черной дыре так близко, чтобы можно было провести подобный эксперимент. Вы не успеете узнать ничего интересного о течении времени, потому что вас раздерут в клочки приливные силы. Это называется спагеттификация — да, представьте себе, это научный термин.

Когда Алиса приблизится к черной дыре, гравитация будет действовать на ее ноги капельку сильнее, чем на голову. Поначалу это не создаст особых трудностей, но чем ближе будет Алиса к черной дыре, тем сильнее станет спагеттификация.

Для сравнения, горизонт событий у черной дыры с массой Солнца примерно три километра — в самый раз для славной оздоровительной прогулки. Если бы мы подвесили Алису в 1400 километрах над горизонтом событий, разница в гравитации между ее головой и ногами составила бы ускорение в 20 g , а человеческий организм такого вынести уже не может.

Оказывается, более или менее независимо от массы черной дыры с точки зрения Алисы пройдет примерно одна пятая секунды от того момента, когда она ощутит заметное неудобство, до того, как ее кости разнесет в пыль.

Однако можно и не мучиться — если черная дыра достаточно велика. Черная дыра массой в 10 000 масс Солнца гораздо безопаснее, чем ее менее массивные сестры. Приливные эффекты так слабы, что Алиса сможет миновать горизонт событий и остаться в живых. Независимо от того, как Алиса попадет туда, если она провалится за горизонт событий, черная дыра станет тяжелее на массу Алисы. Так они и растут.

Наверное, то, как растут черные дыры, требует некоторых разъяснений. Во-первых, черные дыры в большинстве своем не склонны к людоедству. В дикой природе их рацион состоит в основном из пыли, газа, звезд и — в зависимости от размеров — черных дыр поменьше.

Во-вторых, гравитация получается не только из массы. Не забывайте, масса и энергия эквивалентны, поэтому любая разновидность энергии в конечном итоге способна породить гравитацию. Я могу посветить в недра черной дыры фонариком — и она и в самом деле станет чуточку массивнее. Однако у этой медали есть и обратная сторона: испуская излучение, Солнце очень медленно и очень понемногу теряет массу [75] Гораздо больше массы Солнце теряет потому, что непрерывно извергает поток частиц под названием «солнечный ветер», однако крошечную долю потерянной массы действительно составляет потерянная энергия. . Дело просто в том, что масса — самый действенный способ доставить энергию в систему. Правая сторона формулы E = mc² — огромное число даже при небольшой массе, так что нечего удивляться, что вклад массы в гравитацию обычно привлекает к себе больше всего внимания.