Дэйв Голдберг - Вселенная в зеркале заднего вида. Был ли Бог правшой? Или скрытая симметрия, антивещество и бозон Хиггса

Полученная кривая получила название перевернутой циклоиды и очень похожа на обычную миску, только очень точную, математически выведенную.

Все это стало возможным в основном благодаря тому, что лет за десять до этого Исаак Ньютон опубликовал свой трактат « Principia Mathematica ». К тому времени, как Бернулли опубликовал свой вызов, Ньютон уже работал управляющим Королевского монетного двора, однако же нашел время подумать над задачей о брахистохроне. Решил он ее за один вечер перед сном — совсем иначе, чем Бернулли, геометрическим методом. Был он таким математическим врединой, что даже не стал подписываться. Но Бернулли все равно понял, кто это, отметив: «По когтю опознаю льва».

Находить форму кривых в XVII веке было очень модно. Другая знаменитая задача касалась поиска кривой с названием «таутохрона» [55] По-древнегречески буквально «то же время». . Если сделать американские горки такой формы, то откуда бы вы ни пустили вагонетку, она доберется до низу за одно и то же время. Эту задачу решил в 1659 году Христиан Гюйгенс — тот самый, что описал свет как волну. Почему это такое большое достижение, становится понятно, если учесть, что до публикации « Principia Mathematica » оставалось еще почти 30 лет.

Циклоида

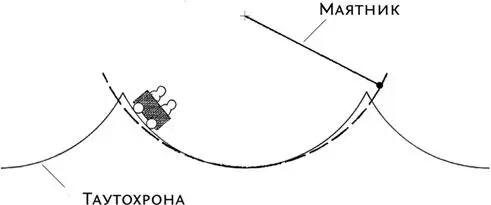
Я заговорил о таутохроне, поскольку выясняется, что она представляет собой точно такую же кривую, что и брахистохрона — циклоиду. Помимо того, что таутохрона — ответ на математическую задачу, она приносит много пользы, поскольку на тех же принципах можно построить и точные часы. На протяжении почти всей мировой истории единственными точными часами на свете было Солнце, а поскольку XVII век был периодом географических открытий и мореплавания, солнечные часы, конечно, уже не годились.

Обратите внимание, что в самом низу таутохрона очень похожа на кривую, которую описывает маятник. И не случайно. Маятники потому и позволяют часам так точно отмерять время, что при условии, что отклонение будет относительно малым, колебания занимают в точности одно и то же время — вот почему дуга маятника так хорошо вписывается в донышко циклоиды. Галилей еще в юности отметил этот факт экспериментально. Ему было скучно, он наблюдал за колебаниями люстры в соборе в Пизе и отметил, что размах колебаний уменьшается, однако время (в ударах сердца) остается постоянным.

Итак, перед нами интересный вопрос: судя по всему, движение частиц, волн и света определяется решениями одних и тех же задач на минимизацию. Найди путь, по которому луч света попадет из точки А в точку В за минимальное время — и надо же, найдешь ту линию, которую он опишет в реальной жизни!

Задачи о брахистохроне и таутохроне показывают, что точно так же можно рассуждать и о движении частиц, обладающих массой. Похоже, минимизация времени в пути — это нечто глубинное и важное.

Ньютон и Бернулли потому-то (отчасти) и были гениями, что сумели решить эти задачи, не располагая никаким общим руководством к решению. В сущности, им пришлось угадывать и перебирать возможные решения, пока они не пришли к идее самого короткого времени.

Все изменилось в XVIII веке, когда Леонард Эйлер и его ученик Жозеф Луи Лагранж обнаружили общее правило, которое позволило им минимизировать по траектории любую величину — хоть время, хоть расстояние.

Не хотелось бы погрязнуть в математике, поэтому давайте вспомним знакомый пример: полет из Филадельфии в Пекин. Возможных путей из одной точки в другую буквально бесконечное множество, хотя большинство из них предполагает извивы и зигзаги. А мы хотим найти простое соотношение, связывающее путь, который нам нужен — то есть тот, который окажется короче всего — с реальностью, в которой нам надо двигаться по выгнутой поверхности Земли.

Эйлер и Лагранж описали способ вычислить кратчайший путь, и неудивительно, что их метод в значительной степени опирался на недавно разработанные Ньютоном методы математического анализа.

Все эти разговоры о минимизации времени хороши, когда мы обсуждаем лучи света, полеты самолетов и американские горки, однако, как выяснилось, все законы Ньютона можно вывести, исходя из тех же предпосылок.

В 1747 году Пьер-Луи Моро де Мопертюи открыл принцип, которому дал название «Принцип наименьшего действия» [56] Хотя лично я убежден, что это название он придумал, чтобы впоследствии студентам-физикам было чем оправдывать малоподвижный образ жизни в колледже. :