Дэйв Голдберг - Вселенная в зеркале заднего вида. Был ли Бог правшой? Или скрытая симметрия, антивещество и бозон Хиггса

Получить все орлы — это уникальный случай. Для такого конкретного макросостояния есть только одно микросостояние, поэтому ситуация и правда особая.

В сущности, энтропия — это количество микросостояний [32] Строго говоря, это логарифм числа вариантов, однако поскольку заниматься вычислениями мы не будем, эта мелочь не должна вас особенно тревожить. Важно лишь одно: для макросостояний, которых можно достичь множеством разных способов, энтропия высока. А если то или иное макросостояние обеспечивают лишь несколько микросостояний, энтропия низка. , в которые могут организоваться частицы или броски монеток, чтобы в результате у вас получилась конфигурация с тем же макросостоянием.

Что именно обеспечивает уникальное макросостояние в системах более хитроумных, чем броски монеток, определить трудновато. К счастью, 1) у нас не учебник математики и 2) для большинства практических целей точное представление о том, как выделить то или иное макросостояние, особенно не влияет на суть аргументации.

Возьмем, к примеру, покер. Существует примерно 2 600 000 комбинаций из пяти карт, которые можно вытянуть из стандартной колоды. Флеш-роялей — главной комбинации карт в покере — из них всего четыре (по одному на масть). Однако вытянуть «старшую карту» или кикер (не стрит, не флеш и не пару) можно более чем полутора миллионами способов. То, какая у вас комбинация (флеш-рояль против кикера) — это макросостояние, тогда как конкретный набор карт — это микросостояние. Энтропия кикера гораздо выше, чем энтропия флеш-рояля.

Ну или порядок у флеш-рояля выше. Но это вы, наверное, и без меня знаете.

А теперь представьте себе, что вы не бросаете монетку и не играете в карты, а взяли четыре молекулы газа и поместили в левую половину коробки. Это очень аккуратный способ хранения с очень низкой энтропией. Теперь предоставьте природе сделать свое дело — и молекулы запорхают во все стороны, причем каждая будет проводить половину времени в левой половине коробки (Л), а половину в правой (П). Можно сделать снимок случайного положения четырех молекул в любой момент. Выстроиться они могут 16 способами, но лишь два из них — ЛЛЛЛ и ПППП — предполагают, что все четыре молекулы окажутся в одной половине коробки. Вероятность такого положения дел всего 12,5 %. Все остальное время молекулы распределены более равномерно. Например, есть шесть способов (37,5 %) рассортировать молекулы так, чтобы в каждой половине коробки их было ровно по две. Равномерное распределение — это более высокий уровень энтропии, чем концентрирование.

Энтропия

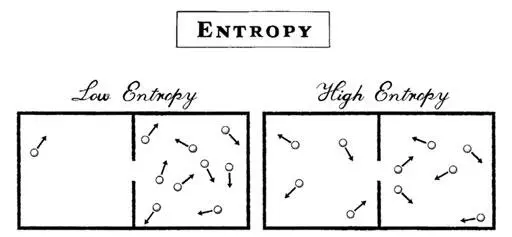
В ту же игру можно играть, если брать все ту же монетку и подбрасывать в воздух. Каждый орел — это молекула в левой стороне коробки и наоборот. Проделайте это много раз — и вы убедитесь, что молекулы почти всегда распределены приблизительно равномерно. Если случайным образом распределять 100 молекул 10 раз в секунду, можно ожидать, что все молекулы окажутся в одной половине коробки, когда пройдет время, приблизительно равное триллиону нынешних возрастов вселенной.

Увеличьте количество молекул, скажем, до 10 28 — количества, способного наполнить небольшую комнату, — и теория вероятности потребует, чтобы случайные движения в конечном итоге привели к равномерному распределению молекул. Если выразить это в числах, то шансы, что обе половины комнаты будут равномерно наполнены воздухом, составляют примерно сто триллионов к одному.

В какой-то момент системы так разрастутся, что уменьшение энтропии станет не просто маловероятным, а до такой степени невозможным, что сама мысль о другом исходе сломает вам мозг. Вот почему так называемый Второй закон термодинамики на самом деле — блестящее предположение . Так что если вы — путешественник по времени, сбившийся с пути, и хотите выяснить, в чем разница между прошлым и будущим, можно просто разобраться, когда энтропия возрастает.

Это не может продолжаться вечно.

Если вся вселенная — всего лишь огромная коробка с газом, в конечном итоге будет достигнуто равновесие, точка, в которой энтропия достигнет максимума и газ распределится между двумя половинами коробки в точности 50 на 50. Когда во вселенной будет максимум энтропии, ей, энтропии, останется только одно — уменьшаться. Молекулы будут и дальше скакать туда-сюда — и нет-нет да и накопится несколько лишних то с одной, то с другой стороны, и тогда энтропия уменьшится . То, что в нашей вселенной есть энтропия, не просто означает, что все распадется — это означает, что способов пребывать в беспорядке гораздо больше , чем пребывать в порядке.