Кип Торн - Черные дыры и складки времени. Дерзкое наследие Эйнштейна

33 [Расчеты показали… на окружности в 1,0001 горизонта.] Ускорение, которое вы почувствуете, зависнув на окружности С над черной дырой с массой М h и окружностью C h, будет а = 4π 2G(M h/C 2)/(l — C h/C) 1/2, где G — гравитационная постоянная Ньютона. Если вы находитесь очень близко к горизонту, то С ≈ C h~ M h, и значит, а ~ 1/ М ь.

33 [При использовании обычного ускорения в lg … по часам звездолета.] См. примечание к с. 30 выше.

36 [Пятно уменьшилось… видим на Земле.] Если зависнуть на окружности С чуть выше горизонта радиусом C h, то свет из внешней Вселенной можно будет увидеть сосредоточенным в ярком диске с угловым диаметром а «З√З√l — C h/C рад ≈ 300√1 — C h/C град. См., например, Врезку 25.7 МТУ.

36-38 [Также необычно то, что цвета… длиной волны 5 х 10 -7метра.] Если зависнуть на окружности С чуть выше горизонта C h, то длина волны света λ из внешней Вселенной будет иметь синеволновое смещение (эффект, обратный красному гравитационному сдвигу) к λ прнято/λ излучеио= √1 — C h/C . См., например, с. 657 МТУ.

42 [Подставив эти числа… через 7 дней.] Когда две черные дыры массой М h каждая обращаются вокруг друг друга на расстоянии D, они имеют период обращения 2π√D 3/2GM h, а сила отдачи испускаемых ими гравитационных волн заставит их сблизиться по спирали и слиться через время (5/512) х (c 5/G 3)(D) 4/M h 3), где, как и выше, G — гравитационная постоянная Ньютона, а с — скорость света. См., например, уравнение (36.17b) в МТУ.

46 [Кольцо имеет длину окружности в 5 миллионов километров… искривления пространства-времени.] Человек, находящийся на собранном из балок кольце, на расстоянии L от внутренней поверхности почувствует ускорение а = (24π 3GM h/C 3)L, направленное к центральному слою, на одну треть вызванное центробежными силами вращающегося кольца и на две трети приливными силами черной дыры. G — гравитационная постоянная Ньютона, M h— масса дыры и С — окружность центрального слоя кольца. Для сравнения гравитационное ускорение на поверхности Земли равно 9,81 м/с 2. См. примечание к с. 27 выше.

48-49 [Законы квантовой гравитации… для путешествия во времени.] 1,62 х 10 -33см = √C/hc 3— длина Планка-Уилера, где G — гравитационная постоянная Ньютона, с — скорость света и h — постоянная Планка (1,055 х 10 -34кг-м 2/с 2). См. главу 14.

51 [Другим фактом… с развевающимися знаменами.] См., например, (Will, 1986).

Общее замечание к главе 1. Большая часть информации о жизни Эйнштейна основана на общеизвестных биографических изданиях: (Pais, 1982; Hoffman, 1972; Clark, 1971; Einstein, 1949;

Frank, 1947). Я не привожу отдельно ссылки на цитаты и факты, взятые из этих источников. Сейчас становятся доступными новые исторические материалы: опубликованы избранные статьи Эйнштейна, ЕСР-1, ЕСР-2, (Einstein and Marie, 1992). Ниже я буду ссылаться на материалы из этих источников.

53 [Профессору Вильгельму Оствальду… Герман Эйнштейн] Документ 99 из ЕСР-1

54 [ «Бездумное поклонение авторитетам есть злейший враг истины»,] Документ 115 в ЕСР-1, согласно переводу на английский (Renn and Schulmann, 1992, с. xix).

55 Сноска 1: Приведем пример того, что означает применять математические выкладки к законам физики:

В начале XVII столетия на основании проведенных Тихо Браге наблюдений планет Иоганн Кеплер вывел, что для всех известных в то время планет: Меркурия, Венеры, Земли, Марса, Юпитера и Сатурна, куб длины орбиты, деленный на квадрат ее периода обращения вокруг Солнца: С 3/Р 2, есть одна и та же величина. Полвека спустя Исаак Ньютон нашел этому объяснение при помощи своих законов движения и тяготения (см. текст на с. 55) и математических выкладок:

1. Из следующей диаграммы, немного попотев, можно получить, что у планеты, вращающейся вокруг Солнца, скорость изменения скорости определяется формулой а= 2πС/Р 2, где π= 3,14159… Эту величину называют центростремительным ускорением обращающейся по орбите планеты.

2. Второй закон движения Ньютона говорит, что центростремительное ускорение должно быть равно силе гравитационного притяжения F g, которая действует на планету со стороны Солнца, деленной на массу планеты М Р, иными словами, 2πС/Р 2= F g/M p.

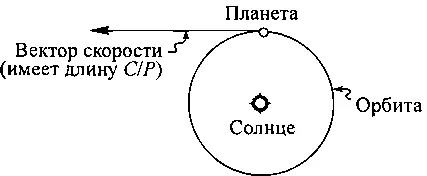
3. Закон тяготения Ньютона утверждает, что сила притяжения F gпропорциональна массе Солнца M s, умноженной на массу планеты М p, деленную на квадрат длины ее орбиты. Если вместо пропорциональности записать точное равенство, то получится: F = 4π 2GM sM p/C 2. Здесь: G — ньютоновская постоянная всемирного тяготения, равная 6,67 х 10 -20км 3/(с 2x кг), или, что то же самое, 1,327 х 10 11км 3/с 2на массу Солнца.