Кип Торн - Черные дыры и складки времени. Дерзкое наследие Эйнштейна

Возьмем червоточину, которая была переделана в машину времени, и разместим два ее устья в межпланетном пространстве, причем оба они будут в покое и рядом друг с другом (рис. 14.9). Допустим, бильярдный шар запускается в правое отверстие с некоторой начальной скоростью из некоторой начальной точки. Шар войдет в правое устье, переместится назад во времени и вылетит из левого устья до того, как он вошел в правое (с точки зрения внешнего наблюдателя). Затем он ударит самого себя, только более «молодого», и таким образом воспрепятствует себе войти в правое отверстие и затем ударить себя.

Эта ситуация, подобно парадоксу матереубийцы, связана с перемещением назад во времени и изменением истории. В парадоксе матереубийцы я возвращаюсь назад во времени и, убив мою мать, не даю самому себе родиться. В парадоксе Полчински бильярдный шар возвращается назад во времени и, ударив самого себя, препятствует своему путешествию во времени.

Обе ситуации не имеют смысла. Законы физики должны логически соответствовать друг другу. Точно так же эволюция Вселенной, управляемая законами физики, должна полностью согласовываться сама с собой — по крайней мере, это будет так, пока Вселенная ведет себя классическим образом (не квантово-механическим); царство квантовой механики более призрачно. Мы с бильярдным шаром — в высшей степени классические объекты (т. е. мы проявляем квантово-механические свойства, только если на нас производить чрезвычайно точные измерения; см. главу 10). Поэтому для нас с бильярдным шаром не существует способа вернуться назад во времени и изменить наши собственные истории. [144] Спустя три года Джону Фридману и Майку Моррису удалось представить убедительное доказательство отсутствия таких парадоксов при путешествии волн назад во времени через червоточину — при условии, что волны накладываются друг на друга линейно (так, как на Врезке 10.3).

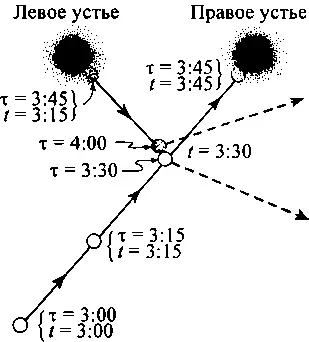
14.9. Бильярдная версия парадокса матереубийцы, придуманная Полчински. Червоточина очень короткая и служит машиной времени, так что любой предмет, который входит в ее правое отверстие, выходит из норы за тридцать минут до своего входа в нее (по часам внешнего наблюдателя). Течение времени вне отверстия обозначается символом г, течение времени, испытываемое самим бильярдным шаром, обозначается буквой t. Бильярдный шар запускается в момент t = 3 часа дня из некоторой точки и именно с той скоростью, чтобы войти в правое отверстие в момент t = 3 часа 45 минут. Шар появляется из левого отверстия на 30 минут раньше, в момент t = 3 часа 15 минут, и ударяет самого себя, более «молодого», в момент t = 3 часа 30 минут дня. Он сталкивает самого себя с траектории и поэтому уже не может войти в правое отверстие, а следовательно, и не ударит себя

Так что же происходит с бильярдным шаром? Чтобы это понять, мы с Моррисом и Юртсевером углубились в изучение начальных условий шара, т. е. его начального местоположения и скорости. Мы спросили себя: «Для тех же самых начальных условий, которые привели к парадоксу Полчински, существует ли какая-либо другая траектория бильярдного шара, кроме изображенной на рис. 14.9, которая являлась бы логически самосогласованным решением и следствием физических законов, управляющих движением классических бильярдных шаров?» После многочисленных дискуссий мы пришли к выводу, что ответ, скорее всего, положительный, но мы не были абсолютно уверены в этом. И у нас уже не было времени это уточнять. Моррис и Юртсевер заканчивали писать свои диссертации и покидали Калифорнийский институт: им удалось получить работу в Милуоки и Триесте.

* * *

К счастью, в Калифорнийском институте не перевелись умные студенты. На подходе были еще двое: Фернандо Эчеверрия и Гуннар Клинкхаммер. Они и подхватили эстафету с парадоксом Полчински.

После нескольких месяцев сложных математических выкладок они доказали, что действительно существует полностью самосогласованная траектория бильярдного шара, в основе которой лежат начальные данные Полчински и которая удовлетворяет всем законам физики, управляющим движением классических бильярдных шаров. По сути дела, есть две такие траектории. Они показаны на рис. 14.10. Я опишу каждую из этих траекторий по очереди, с точки зрения самого шара.