В строительстве величественного здания общечеловеческой культуры теории информации предстоит выполнять роль цемента. В самом деле, «величественное здание физики», которое, по мнению Сноу, строится особняком от гуманитарных наук и искусства, для энтропии теперь стало слишком мало. Ведь с помощью энтропии теперь решаются не только физические проблемы. Благодаря теории информации энтропия стала эффективно использоваться и биологией, и психологией, и лингвистикой, и искусствоведением, и... В общем, сейчас трудно даже назвать область знаний и творчества, для которых не был бы актуален новый энтропийно-информационный подход.
Будем надеяться, что после всего сказанного читатель не захлопнет в сердцах эту книгу, встретив в очередной раз пока еще непонятные ему математические символы. По крайней мере он попытается прежде приложить немного усилий, чтобы понять, в чем заключается смысл замечательной функции энтропии и что таят в себе ее «каббалистические» знаки. Тем более что усилий нужно не так уж много, поскольку теория информации пролила на энтропию достаточно яркий свет. Благодаря теории информации наука стала исследовать энтропию не только незримых микропроцессов, но и таких доступных для непосредственных наблюдений объектов, как изображение на телеэкране или печатный текст.
Больцману было много труднее, поскольку с помощью этой функции он исследовал не доступный непосредственным наблюдениям, а лишь воображаемый микромир. И все же ему удалось «увидеть», как в таком мире ведет себя энтропия: она возрастает в том случае, если вероятности всех скоростей и положений молекул приближаются друг к другу. Так, например, разбив мысленно все занимаемое газом пространство на N равных по объему ячеек, можно утверждать, что энтропия достигнет максимума, когда все молекулы равномерно распределятся по всем N ячейкам.
Переходя на язык теории вероятностей, можно сказать: энтропия достигнет максимума, когда вероятность нахождения молекулы в 1-й ячейке равна вероятности нахождения ее в 5-й ячейке или в любой другой ячейке из общего числа N. Обозначив через p i вероятность того, что молекула находится в i-й ячейке, и считая, что i может принимать любые значения от 1 до N (i=1, 2, 3, ..., N), запишем условие максимального значения энтропии, соответствующее наиболее беспорядочному, хаотичному расположению молекул в ячейках p 1=p 2=...=p i=p N
При таком условии функция 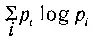 имеет наибольшую величину
имеет наибольшую величину [3] Создавая вероятностную теорию энтропии, Больцман рассматривал не только реальное пространство, но и условное «пространство скоростей». Он показал, что скорости молекул (так же как и сами молекулы) стремятся равномерно «заполнить предоставленное им пространство». Когда газ достигает состояния равновесия, распределение вероятностей скоростей подчиняется нормальному закону, описываемому формулой и кривой Максвелла.
.
В этом как раз и заключается ее главное свойство и, если угодно, ее безграничная (распространяющаяся на всю Вселенную!) вездесущая роль.
Как видите, уяснить математические свойства функции , в общем-то, не так уж и сложно. Гораздо труднее, как уже говорилось, уяснить ее общенаучный смысл. Споры об этом, разгоревшиеся во времена Больцмана, еще с большим накалом продолжаются в наши дни. Тому причиной новое применение функции в теории информации.
Вот пример «энтропийного» текста, то есть текста, в котором появление любой буквы имеет равную вероятность ( р А= р Б= ... = р Я ). Он выглядит так: СУХЕРРОБЬ ДЩ ЯЫХВЩИЮАЙЖТЛФВНЗАГФОЕНВШТЦР ПХГ БКУЧТЖЮРЯПЧЬКЙХРЫС. Полная абракадабра! Ничего удивительного. Этот текст обладает максимальной энтропией, а энтропия, как мы уже уловили, есть выражение хаоса, будь то хаос беспорядочно сталкивающихся друг с другом молекул, или хаос звуков, воспринимаемых в виде шума, или хаос бессмысленно чередующихся букв.
НЕСПРАВЕДЛИВОСТЬ. ОТ БОЛЬЦМАНА ДО ШЕННОНА. БАНДВАГОН ОТ НАУКИ. ДВИЖЕНИЕ БЕЗ ТРЕНИЯ И ИНФОРМАЦИЯ БЕЗ СМЫСЛА. ДЖИНН ПОКИДАЕТ БУТЫЛКУ. ЗАПРЕТИТЕ РАДИОСВЯЗЬ!
Современный ученый произносит имя Больцмана с глубоким почтением. Работы Больцмана послужили фундаментом современной статистической физики. На них опирался Клод Шеннон, предложивший использовать для измерения информации введенную в науку Больцманом функцию В этой связи Шеннон вспоминает о Больцмане в своих первых работах по теории информации, которые (редчайший случай в науке!) стали классическими, едва успев выйти в свет.
Читать дальше

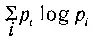 имеет наибольшую величину
имеет наибольшую величину 








