Юрий Козлов - Общая теория всего физического мира

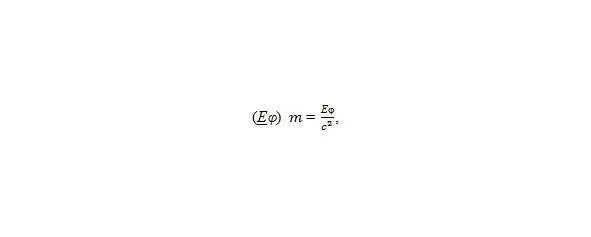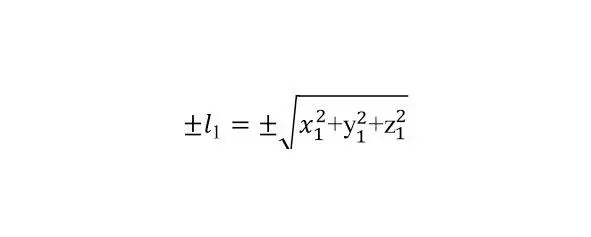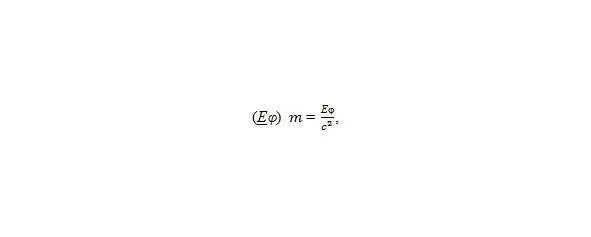
на нулевом радиусе черной дыры (r 0) – множество точек, равноудалённых от центра системы. Проще говоря, вокруг черной дыры должно вращаться торсионное поле, замыкаясь в петлю нулевого времени на нулевом радиусе. Поле должно удерживаться на орбите гравитацией черной дыры (динамичная структура). Моменту рождения положительной массы, согласно общей теории относительности (ОТО), соответствует область пространства с нулевым пространственно-временным интервалом (S 2 0,0 = 0), где масса, пространство и время имеют нулевые значения, а скорость равна скорости света (m 0= 0; t 0,0 = 0; l 0,0 = 0; v = c).

В этом ракурсе постараемся описать ОСНОВЫ ТЕОРИИ АНТИГРАВИТАЦИИ, когда масса, пространство и время принимают отрицательные значения, скорость движения частиц материи выше скорости света, а главное – показать ту строго очерченную зону внутри каждой галактики, где это неизбежно (за нулем координат внутри черной дыры). В общей теории относительности такое положение вещей свойственно областям пространства с отрицательным пространственно-временным интервалом (S 2 —1,0 <0). Сегодняшняя физика отрицает наличие таких пространств в масштабах нашей Вселенной. Мы же постараемся убедить даже читателя-пессимиста в том, что такие области пространства с неизбежностью существуют как внутри каждой галактики, так и внутри каждого атома. Если предлагаемые доводы достаточно аргументированы (аргументов можно добавить), то эта маленькая статья сподвигнет научную элиту общества к грандиозному скачку в понимании Мироздания.

Однако дадим возможность специалистам разобраться в математической интерпретации физики предлагаемой гипотезы, при этом отметим возможность возврата к классической механике Ньютона. Тогда при расчетах внутри галактической системы возможно использование простых формул преобразований Галилея вместо сложных формул преобразований Лоренца, требующих замены тригонометрических функций гиперболическими.

Предлагаемая гипотеза утверждает, что в связи с нахождением черной дыры в центре системы (МА), ее пространственные и временные координаты для данной обособленной системы равны нулю на нулевом радиусе (при S 2 0,0 = 0; l 0= r 0= 0; t 0= 0) в точках М 0.Расстоянию между событиями происходящими в точках M -1 и М 0или М 0и M 1: +l 0,1 (при S 2 0,1>0) или - l -1,0 (при S 2 —1,0 <0) будет соответствовать: l 0,1 = l 1 – r 0 или – l -1,0 = – l -1 – r 0 . Справедливо развернуть l 1и – l -1 в пространственные координаты:

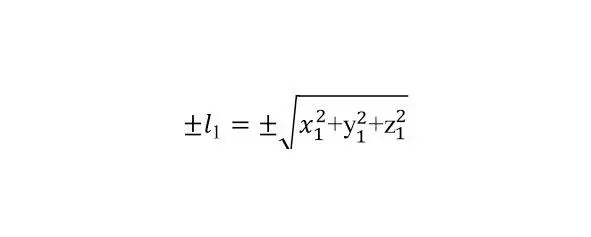
(6)

где: x 1, y 1, z 1 – пространственные координаты фиксированной точки.

Каждой точке пространства в системе МА всегда соответствует вполне определенное расстояние, однако фиксированному расстоянию в системе МА соответствует множество точек, находящихся на части поверхности шара (R = ± l ), равноудаленных от центра системы.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.