Дэниэл Деннет - Насосы интуиции и другие инструменты мышления [litres]

В моем эссе “Куайнирование квалиа” (1988a) я описываю целых четырнадцать насосов интуиции, призванных прояснить и затем опровергнуть безнадежно запутанную философскую концепцию квалиа. В эту книгу вошел лишь один из них, “Проклятие цветной капусты”. Он помогает мне ввести понятие и познакомить читателей с серьезной проблемой квалиа. Я рекомендую прочитать “Куайнирование квалиа” всем тем, кто по-прежнему считает концепцию квалиа (как ее называют философы) состоятельной. Эссе не раз включалось в разные антологии и доступно в интернете на нескольких языках. В моей книге “Сладкие сны” (2005b) содержатся другие аргументы и насосы интуиции по теме. Среди других насосов интуиции о сознании можно выделить “амнестический кураре” в эссе “Почему нельзя создать компьютер, чувствующий боль” (Dennett 1978c), “Болотная Мэри и робот Мэри” в эссе “Что знает робот Мэри” (Dennett 2007d), а также “оруэлловскую и сталинскую” модели сознания в книге “Объясненное сознание” (Dennett 1991a). Все они требуют более тщательной подготовки мизансцены, чем я мог себе позволить, ибо мне не хотелось, чтобы эта книга не стала слишком длинной.

Я также не включил сюда насосы интуиции для мышления о религии, которые предложил в эссе “Рассеивая чары” (Dennett 2006a), и мой пример с Суперменом, подправляющим сланцы Бёрджесс, приведенный в книге “Наука и религия. Совместимы ли они?” (Dennett, Plantinga 2011).

программа 1:

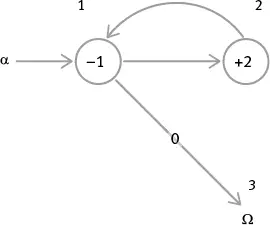
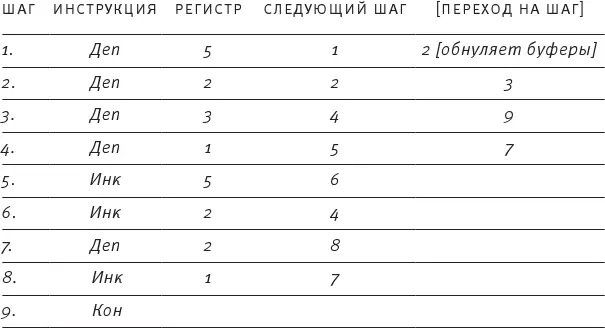
а. Сколько шагов потребуется регистровой машине, чтобы сложить 2 + 5 и получить 7 , выполняя программу 1 (считая Кон отдельным шагом)?

Ответ: шесть шагов. Три декремента, два инкремента, одно окончание программы (последний декремент – переход на ноль).

б. Сколько шагов потребуется машине, чтобы сложить 5 + 2?

Ответ: двенадцать шагов. Шесть декрементов, пять инкрементов и одно окончание программы.

1 (Какой из этого можно сделать вывод?)

Ответ: порядок содержимого может иметь большое значение, так что вам может показаться необходимым ввести правило всегда помещать меньшее число в регистр 1, но, если для этого вам сначала придется сравнивать два числа, чтобы выяснить, какое из них меньше, в итоге вам потребуется больше шагов, чем для сложения!

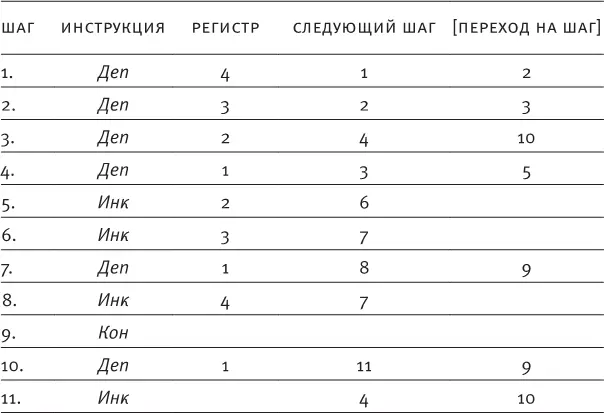
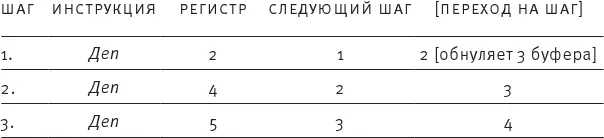
а. Напишите РПА-программу для этого графа потока. (Обратите внимание: поскольку программа разветвляется, вы можете пронумеровать шаги несколькими способами. Неважно, какой из них вы выберете: главное, чтобы на верные следующие шаги указывали команды безусловного перехода.)

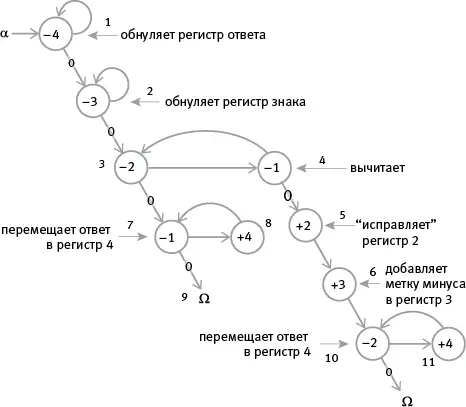
б. Что происходит, когда программа пытается вычесть 3 из 3 или 4 из 4?

Программа останавливается с нулем в регистре 4.

в. Какая возможная ошибка предотвращается обнулением регистра 3 перед попыткой вычитания на шаге 3 вместо шага 4?

Если на старте и в регистре 1, и в регистре 2 были нули, в конце программа могла выдать абсурдный ответ (либо – 0, либо число, отличное от 0 и 1, в регистре знака).

а. Нарисуйте граф потока (и напишите РПА-программу) для умножения содержимого регистра 1 на содержимое регистра 3 , поместив ответ в регистр 5.

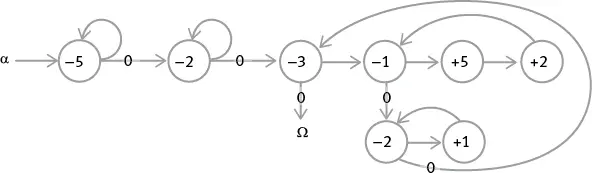
б. (По желанию) Используя копирование и перемещение, улучшите программу умножения, созданную в задаче а: когда она закончит работу, изначальное содержимое регистра 1 и регистра 3 восстановится, так что вы сможете легко проверить исходные данные и ответы на правильность по завершении программы.

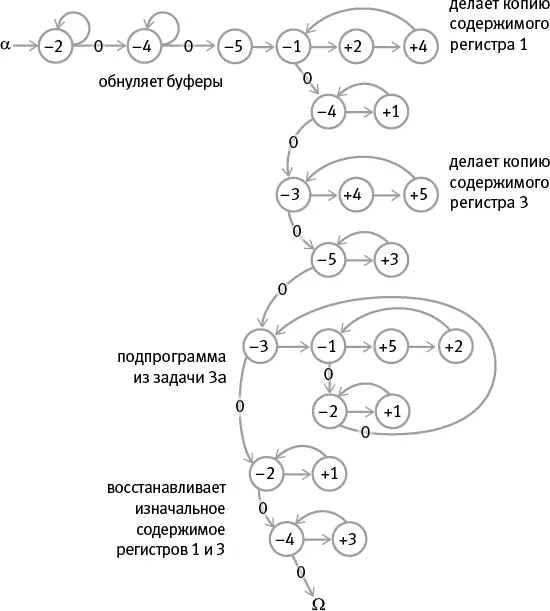
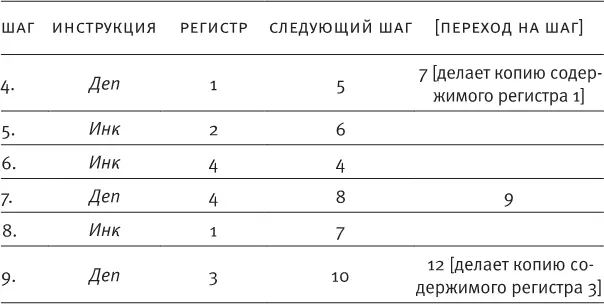
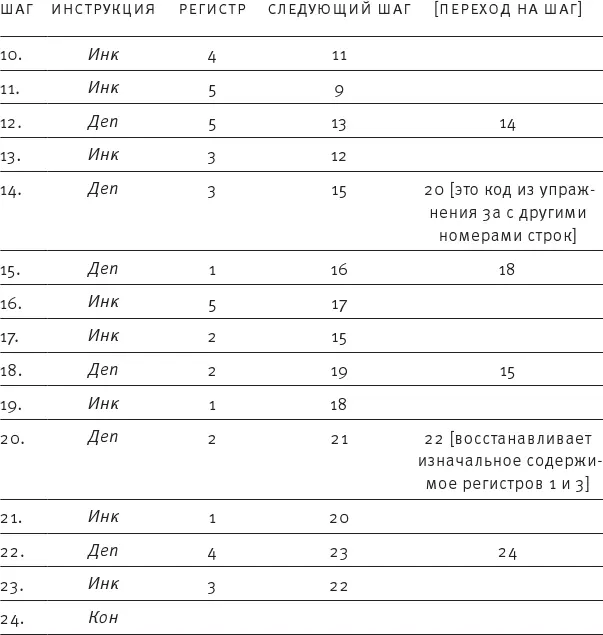
в. (По желанию) Нарисуйте граф потока и напишите РПА-программу, которая изучает содержимое регистра 1 и регистра 3 (не разрушая их!) и записывает адрес ( 1 или 3 ) регистра с большим содержимым в регистр 2 или помещает 2 в регистр 2 , если содержимое регистров 1 и 3 равно. (После выполнения этой программы содержимое регистра 1 и регистра 3 должно остаться неизменным, а регистр 2 должен показывать, равно ли их содержимое, а если нет, то в каком из регистров содержимое больше.)