Об ошибках такого рода говорят: «Кто слишком мало доказывает, тот ничего не доказывает». Именно такая сшибка имела место в приведенном выше доказательстве того, что средняя школа не должна давать даже простейших навыков в области высшей математики. Доказывая это, ссылаются на то, что для изучения высшей математики в вузе важнее другие разделы. Но в данном случае решается вопрос об изучении математики не только теми учащимися, которые будут поступать в технические вузы, но и теми, которые пойдут в другие вузы, и теми, которые вообще не будут поступать в вуз. Может быть, именно для тех, кто изучает математику только в средней школе, особенно важно ознакомление с некоторыми разделами высшей математики. Во всяком случае, это необходимо каждому учащемуся уже для того, чтобы иметь более или менее ясное представление о тех предметах, среди которых он будет выбирать свою будущую специальность. Обосновывать ненужность изучения элементов высшей математики в средней школе тем, что они не обязательны для будущих студентов технических вузов, — это значит вместо данного тезиса доказывать лишь его часть.
Подмена тезиса особенно часто наблюдается при опровержениях , когда обосновывается не истинность, а ложность какого-либо утверждения. В этих случаях очень часто опровергается совсем не то, что нужно опровергнуть.
Открытие сложного строения атома показало, что материя не обладает теми свойствами непроницаемости, твердости, неделимости и т. д., которые ей приписывались прежними философами-материалистами. В связи с этим идеалисты объявили опровергнутым материализм вообще. Но в этом отношении опровергнут был не материализм вообще, а только старый, так называемый метафизический материализм. Новый же, диалектический материализм, созданный К. Марксом и Ф. Энгельсом, этими открытиями не только не был опровергнут, но, как показал В. И. Ленин в работе «Материализм и эмпириокритицизм», нашел в них свое блестящее подтверждение. Опровергая материализм вообще на основе опровержения метафизического материализма, идеалисты подменяли один тезис другим.
Подмена тезиса при опровержении довольно часто наблюдается и в обыденной жизни. Нередко можно услышать разговор такого типа:
А. Книгу, которая нам нужна, могут до завтра продать, так что пойдем в книжный магазин сегодня.
Б. Нет, ее продать не могут.
На следующий день книга оказалась непроданной, По этому поводу Б. замечает: «Вот видишь, а ты говорил, что ее продадут».
Тот факт, что книгу не продали, опровергает утверждение «книгу обязательно продадут». Но А. утверждал только, что книгу могут продать, и это утверждение фактом наличия книги не опровергается. Утверждая обратное, Б. подменяет один тезис другим.
Теперь посмотрим, каким требованиям должна удовлетворять вторая часть доказательства — аргументы, для того чтобы доказательство было правильным.
Прежде всего положения, которые приводятся в качестве аргументов, должны быть безусловно истинными . Это одно из самых важных правил доказательства. Если умозаключение в принципе может быть правильным даже при наличии фактических ошибок в посылках, то обязательным условием логической правильности доказательства является фактическая истинность посылок.
Ошибка, связанная с нарушением этого правила, была допущена в приведенном выше доказательстве того, что не существует антиподов. Авторы этого рассуждения исходили из ложной предпосылки о существовании абсолютного, одинакового для всего мира «верха» и «низа», что обусловило логическую несостоятельность этого доказательства. Поэтому совершенно неправильно мнение, согласно которому это рассуждение «логично, но… ошибочно».
Здесь доказательство смешивается с умозаключением. Можно строго логично сделать вывод из ложных суждений, но нельзя доказывать ложным суждением. Ошибочность посылки означает нелогичность доказательства.
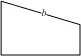
Рис. 9

Рис. 10
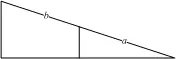
Рис. 11
Ошибка, связанная с неистинностью аргументов, носит название «основного заблуждения», то есть заблуждения, лежащего в основании. Ее иногда бывает трудно обнаружить в связи с тем, что трудно выделить самые аргументы. Аргумент маскируется, упоминается мимоходом, благодаря чему маскируется и логическая ошибка. Так было замаскировано одно из неправильных исходных положений в доказательстве того, что 441 см 2= 442 см 2. В этом доказательстве исходят из того, что если сложить вместе прямоугольную трапецию (рис. 9) и прямоугольный треугольник (рис. 10), то получится прямоугольный треугольник, то есть сторона « a » треугольника будет продолжением стороны « b » трапеции (рис. 11). Но этот аргумент вовсе не очевиден. Мало того, при указанных в задаче размерах он является ложным. Если бы треугольник и трапеция соответствовали данным размерам, то от их сложения получился бы не треугольник, а четырехугольник (рис. 12). При тех размерах, которые даны в задаче, разница оказывается настолько незначительной (в конечном итоге — всего лишь 1 см 2), что заметить ошибку на чертеже почти невозможно. Но с логической точки зрения тот факт, что при рассуждении исходили из положения, истинность которого не проверена, делает все доказательство неправильным.
Читать дальше









![Ив Жангра - Ошибки в оценке науки, или как правильно использовать библиометрию [калибрятина]](/books/390964/iv-zhangra-oshibki-v-ocenke-nauki-ili-kak-pravilno-thumb.webp)
![Александр Силаев - Философия без дураков [Как логические ошибки становятся мировоззрением и как с этим бороться?] [litres]](/books/393881/aleksandr-silaev-filosofiya-bez-durakov-kak-logiche-thumb.webp)




