Хаймо Хофмайстер - Что значит мыслить философски [Поиск фундамента всего знания и всего сущего]

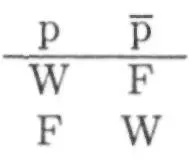
В классической, т. е. двойственной логике, для которой существуют только два значения, а именно «истинное» или «ложное», оба этих значения соотносятся друг с другом как альтернативы. Чтобы пояснить это, мы обратимся к высказыванию: «Собор Святого Стефана находится в Вене». Это высказывание может быть истинным или ложным. Если оно ложно, то истинно высказывание «Собор Святого Стефана не находится в Вене». Обозначим первое высказывание как «р», второе — как «не-р» (р). Если принять для истинного и ложного буквы W и F, то мы сможем отношение двух взаимоисключающих высказываний записать таким образом:

Если связать два высказывания друг с другом выводом, то мы должны, поскольку оба высказывания обладают истинным значением, задаться вопросом, каким образом истинное значение вывода, из связи которого возникает новое высказывание, соотносится с истинным значением связанного высказывания. [295]Два связанных высказывания, часто называемые: одно — «функтор», второе — «юнктор», объединены. Эти функторы или юнкторы обозначаются как «и», «или», «если, то», «или, или». Это можно наглядно продемонстрировать на примере: остановимся на высказывании «Собор Святого Стефана находится в Вене, а Штутгарт является столицей земли Баден-Вюртемберг». Истинное значение этого высказывания зависит от истинного значения высказывания «Собор Святого Стефана находится в Вене» (р) и высказывания «Штутгарт является столицей земли Баден-Вюртенберг» (q). Юнктор «и», который связывает оба высказывания, исключается с помощью символа «Λ». Применяя символический юнктор и знаки ρ и q, мы можем сказать:

Если истинно ρ и истинно q, то истинно pΛq.

Если ρ истинно, a q — ложно, или, соответственно, ρ ложно, a q истинно, то ложно также и pΛq.

Если ложно ρ и ложно q, то ложно также и pΛq.

Связь двух высказываний юнктором «Λ» дает «конъюнкцию». Графически это выглядит так:

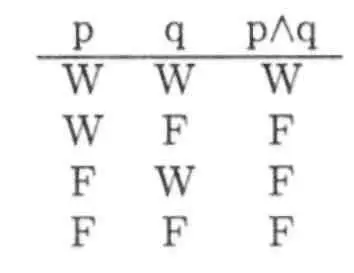
Это конъюнкция.

Наряду с конъюнкцией существуют дизъюнкция (pVq), импликация (p→q), исключение (p|q) и эквивалентность (p↔q). Примером дизъюнкции служит следующее высказывание: «Он ехал на автомобиле или на велосипеде». Это высказывание истинно, если одно из двух высказываний истинно (правда, немецкое слово «или» многозначно: если я говорю «X является врачом или профессором», то это «или» допускает одно из двух, но в то же время то и другое). Импликация выражает отношение «если… то»: «Если Вена стоит на Дунае, то Гейдельберг — на Неккаре». Импликция только тогда ложна, когда первое высказывание истинно, а второе — ложно, и она истинна, если первое высказывание ложно и второе также ложно. При исключении не могут быть одновременно истинными оба высказывания, примером тому может служить следующее предложение: «Ортлер — самая высокая гора в Австрии и Южном Тироле». Ортлер не может быть в двух местах, так как Южный Тироль отделен от Австрии, к тому же не является границей между ними. В исключении нет двух высказываний ни истинных, ни ложных. Эквивалентность в обиходе описывается подобно импликации словом «если» и часто подразумевает следующее:

«Ортлер является самой высокой горой Австрии в том случае, если Южный Тироль находится в Австрии». Другой пример звучит так: «Если день Святого Стефана (26 декабря) выпадает на воскресенье, то наступающий Новый год падает на субботу».

Логика построена на различных основоположениях, которые, хотя сами и не выведены, т. е. не доказаны, становятся в свою очередь предпосылкой выведения других предложений, так называемых теорем. Эти основоположения считаются в классической логике наиболее общими законами, которые имеют значение для всякого высказывания. В символической же логике или логистике, в противоположность этому, они считаются только базисными формами, из которых могут быть выведены все теоремы и к которым они могут быть сведены. Для классической логики основоположения являются безусловными и потому не требуют доказательства. Для современной логики они таковыми не представляются, и требуются доказательства для принятия решения об их эффективности как базисных форм. И далее, они для нее уже не единственные базисные формы. Есть еще и такие, которые имеют значение только в рамках этой логики.