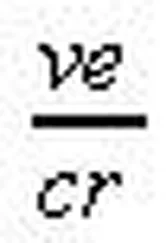Алексей Лосев - Очерки античного символизма и мифологии

Для Пифагора число — оптический символ, не форма вообще или абстрактное отношение, «но разграничивающий признак ставшего, поскольку последнее п–роявляется в чувственно обозримых подробностях». «Вся античная математика в основе своей есть стереометрия ». Для Эвкли–да треугольник всегда есть поверхность, ограничивающая тело, но никак не определенная система трех ли ний или трех точек. Линию он определяет как «длину без ширины». «При нашем способе выражаться это определение показалось бы убогим. В границах античной математики оно превосходно». В связи с этим делается понятным, почему античность знает только «естественные», т. е. положительные и целые, числа, что представляет собой полную противоположность сложным западным учениям о комплексных, гиперкомплексных, неархимедовых системах. По Эвклиду, несоизмеримые расстояния относятся между собой «не как числа». «Действительно, в законченном понятии иррациональных чисел лежит полное отделение понятия числа от понятия величины ; причина этому та, что иррациональное число, напр. π, никогда не может быть отграничено или точно выражено при помощи известного расстояния. Из этого следует, что, напр., в представлении об отношении стороны квадрата к его диагонали античное число, представляющее собой собственно чувственную границу, замкнутую величину и не что иное, соприкасается с совершенно иной числовой идеей, в самой своей сути чуждой античному мирочувствованию и поэтому жуткой, как будто бы дело идет о том, чтобы вскрыть опасную тайну собственного существования. На это указывает позднегрече–ский миф, согласно которому тот, кто впервые извлек рассмотрение иррационального из сокровенности и предал его гласности, погиб при кораблекрушении, так как невыска–зываемое и безобразное должно постоянно оставаться сокровенным». Античная математика — система, выросшая на привязанности к телу и на метафизическом страхе выйти из пределов того тела. «Кто поймет страх, лежащий в основе этого мифа, — тот же страх, который постоянно удерживал греков зрелого времени от расширения их крю–хотных городов–государств в политически организованные страны, от устройства широких проспектов и аллей с далеким видом и рассчитанным завершением, от вавилонской астрономии с ее устремлением в бесконечные звездные пространства, от преодоления границ Средиземного моря и исследования путей, давно открытых кораблями египтян и финикиян, эту глубокую метафизическую боязнь перед преодолением осязательно–чувственного и настоящего, при помощи которого античное существование окружило себя как бы защитной стеной, за пределами которой лежало что–то жуткое, бездна и первоисточник в известной мере искусственно созданного и утвержденного космоса, — кто поймет это чувство, тому станет понятной основная сущность античного числа, являвшего собой меру в противоположность неизмеримому , а также глубокий религиозный этос, выражающийся в этом ограничении» [46] Там же, 75—76. .

Полной противоположностью античному пониманию числа является западное понимание, основанное на категории не величины и меры, но отношения и функции . «Вместо чувственного элемента конкретного отрезка прямой линии и поверхности — специфического выражения античного чувства предела — появляется элемент отвлеченно–пространственный и таким образом совершенно не античный элемент точки , характеризуемой отныне как группа сопряженных чистых чисел. Декарт разрушил литературно унаследованное понятие величины, чувственных размеров и заменил его изменяющейся значимостью отношений положения в пространстве. Однако упускают из виду, что это было равносильным упразднению геометрии вообще, которая с того времени среди мира чисел анализа ведет только призрачное существование, завуалированное античными реминисценциями. В слово «геометрия» вложен неустра–няемый аполлоновский смысл. После Декарта так называемая «новая геометрия» превратилась или в синтетический процесс, определяющий посредством чисел положение точек в каком–нибудь пространстве, притом не обязательно трехмерном (в некоторой «множественности точек»), или в аналитический процесс, определяющий числа положением точек. Заменять отрезки прямой положениями значит воспринимать понятие протяженности чисто пространственно, но уже не телесно» [47] Там же, 85. . «Если определять античный мир, космос, исходя из его внутреннего требования видимой границы, как исчисляемую сумму материальных предметов, то, со своей стороны, наше мирочувство–вание находит свое выражение в образе бесконечного пространства, в котором все видимое воспринимается как нечто обусловленное по отношению к чему–то безусловному или даже, пожалуй, как действительность низшего порядка. Его символом является решающее, ни в какой другой культуре не встречающееся понятие функции. Функция не есть какое–то расширение одного из ранее имевшихся числовых понятий; она является их полным преодолением. Таким образом, не только эвклидовская, т. е. общечеловеческая популярная, геометрия, но и архимедовская сфера элементарного счисления, т. е. арифметика, перестают существовать для действительной обладающей значением математики Западной Европы. Остается один отвлеченный анализ. Для античного человека геометрия и арифметика были научными комплексами высшего порядка, причем и та и другая были наглядными и обращались с величинами при помощи графических и счетных приемов; для нас они только практические пособия повседневной жизни. Сложение и умножение, эти два античные метода счисления величин, родственные графическому конструированию, совершенно исчезают в бесконечности функциональных процессов. Так, напр., степени, по своему принципу являющиеся первоначально просто числовыми обозначениями определенных групп умножений (для множителей одинаковой величины), при посредстве нового символа показателя степени (логарифм) и способа его применения в комплексных, отрицательных и дробных формах становятся совершенно отрешенными от понятия величины и переносятся в трансцедентальный мир отношений, который для грека, знавшего только две целые степени в качестве изображения поверхности и тела, является совершенно недоступным (стоит только припомнить такие выражения, как е –х, n√x, a1/i)». [48] Там же, 85—86.