Юрген Аппело - Agile-менеджмент. Лидерство и управление командами

С учетом этих пяти аргументов я беру на себя смелость утверждать, что многие живые системы действительно со временем становятся более сложными. Мне никогда раньше не приходило в голову, что я когда-нибудь буду несогласен с Гулдом, поскольку мне он всегда казался одним из самых умных людей на планете. И все же я вынужден с ним не согласиться. Так что вполне возможно, что прогресс все-таки существует.

Когда мне было пятнадцать, я увлекался чтением книг, в которых рассказывалось о пространстве и форме Вселенной. (Мои сверстники больше интересовались совсем другими формами, но мне всегда хотелось разобраться в общей картине.) То, что я прочитал о специальной теории относительности и расширяющейся Вселенной, побудило меня нарисовать на листе бумаге свой собственный четырехмерный объект (рис. 14.5).

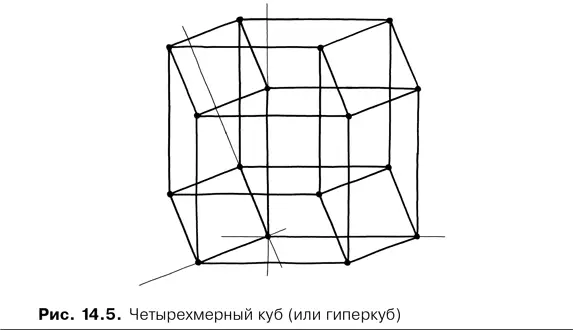
Я построил объект, изображенный на рис. 14.5, переместив обычный куб в воображаемом четырехмерном пространстве и соединив шестнадцать углов линиями, точно так же, как мы можем построить обычный куб, сдвинув квадрат в трехмерном пространстве и соединив линиями восемь углов. Я был упоен тем, что так просто нарисовать 2D-проекцию 3D-проекции 4D-объекта. В то время данная фигура мне нравилась больше всего. Но когда я показал свой рисунок учителю физики, тот сказал мне, что все нарисовано неправильно. Мне казалось, что меня не поняли. Годы спустя я узнал, что объект, который я «изобрел», называется гиперкуб и что учитель физики упустил прекрасную возможность чему-то научиться у одного из своих учеников.

Но гиперкуб – ничто в сравнении с «формой улучшения» сложной системы. Оценивая разные состояния динамической системы, исследователи представляют каждую переменную систему как ось многомерной Вселенной. Небольшая система с тремя переменными отображается в виде фазового пространствас тремя измерениями; у системы с двадцатью переменными фазовое пространство имеет не менее двадцати измерений. Боюсь, что даже я не смогу нарисовать такой объект. И это еще не предел. Многие сложные системы содержат тысячи и более переменных и соответствующее ошеломляюще сложное фазовое пространство.

Например, у водорослей порядка 1000 генов. Предположим ради простоты, что каждый из этих генов отвечает за два признака: листья могут быть зелеными или коричневыми, маленькими или большими, плоскими или морщинистыми и так далее. В этом случае число возможных состояний конкретного растения будет составлять 21000, или тысячу измерений по два возможных значения в каждом из них [Waldrop 1992: 167]. (ДНК человека состоит примерно из 25 000 генов – и более чем двух вариантов каждого. Можете себе представить гиперкуб, нарисованный в таком фазовом пространстве?)

Конкретное состояние системы отображается одной точкой в ее фазовом пространстве. (У каждой переменной в данный момент может быть только одно значение.) Когда одна из переменных изменяется, говорят, что система движется в своем фазовом пространстве. Переключение одного гена в ДНК водорослей (например, переход с зеленых листьев на коричневые) сдвигает ДНК из одной точки в ее фазовом пространстве в соседнюю. А одновременное изменение многих переменных (например, в случае смешивания цепочек ДНК из женского организма и мужского с получением на выходе новой ДНК) будет уже гиперпрыжком в фазовом пространстве.

Представляя изменения в виде перемещения в пространстве, легче визуализировать и обсуждать закономерности непрерывной оптимизации. Также становится яснее, какие формы важны, а какие – нет.

Усложним немного нашу математику. Наберитесь терпения, я постараюсь помочь вам пройти этот нелегкий путь. Пейзаж, который откроется вашему взору, оправдает приложенные усилия.

Когда сложные системы изменяются, их путешествие в соответствующем обширном фазовом пространстве обычно попадает в одну из нескольких категорий. Вспомните пример с игрой «Жизнь», описанной в главе 8. Независимо от исходной конфигурации, через несколько этапов система в большинстве случаев приходит в устойчивое состояние, которое будет либо стационарным («натюрморт»), либо бесконечно повторяющимся циклом небольшого числа состояний. Мы говорим, что устойчивое состояние – это аттрактор для всех других состояний, которые к нему приводят. Набор всех траекторий, которые приводят к данному аттрактору, называется областью притяжения аттрактора(рис. 14.6). Поскольку каждая система обычно следует по траекториям, которые ведут к аттракторам, аттракторы затягивают систему в один небольшой регион ее фазового состояния. Несмотря на огромное число возможных состояний системы, она в конечном итоге оказывается лишь в одном из немногих упорядоченных состояний.