V. Dontsov - General system theory of aging. Special role of the immune system

The relationship of order and chaos can be represented in the form of a general scheme, reflected in Figure 2 .

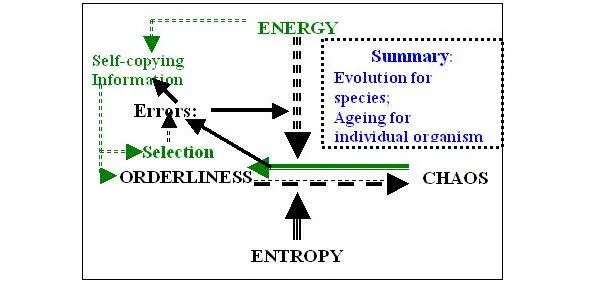
Figure 2. The relationship between the processes of order and chaos.

In general, the processes of disintegration of any system are guided by the law of increasing entropy in the course of naturally occurring processes, which leads to an increase in chaos and a decrease in order in the system. The only way to resist the processes of entropy accumulation is external energy. External energy is necessary to obtain an order from chaos, but it operates under specific conditions, according to a specific plan, based on information from biological systems (development based on the organism’s genetics), and by self-copying of existing biomolecules and biostructures.

The order (structure) of the system spontaneously (according to the law of increasing entropy) turns into chaos. This is opposed by the external energy, based on information (internal to the biological system) restoring the order (structure) of the system (by self-copying). Entropia also distorts this process, leading to errors. Errors of the (self) recovery of the system are controlled by selection: external and internal (by the immune system, etc.). The result is a constant dynamic process that ensures not only the constant preservation of the system, but its dynamic equilibrium and, if necessary, evolution.

Entropy counteracts this process through errors that inevitably manifest themselves at all and at all levels of system organization. Errors are confronted by selection (natural selection for the species and the immune and other mechanisms inside the body), however, the selection is also subject to inevitable errors and provides only material for the evolution of the system (organism).

In practice, it is impossible to achieve infinite evolution and complication within the organism, as is the case for species and the entire biosphere. In addition, due to the very existence of the organism as a separate system, the organism is fundamentally mortal, and selection and evolution do not have enough time and necessity (as well as opportunities) to form an ageless organism in which all errors are fully compensated inside it and full evolution and further infinite development occur. In fact, the inevitable accumulation of errors, cessation of development and reduction of orderliness in general, which is the aging of living organisms. The most important general point is that the very existence of the system is not stationarity and immutability, but a dynamic process that is in equilibrium with the external environment.

The decrease in the general metabolism known with age, the decrease in the reactivity and stability of the organism can be interpreted unambiguously as a decrease in the “openness” of the system, its renewability, and connection with the external environment. At the biochemical level, an increase in entropy is also manifested in a decrease in the orderliness of the network of metabolism, a decrease in the level of exchange of macromolecules (DNA repair in the first place), the accumulation of “errors” (including mutations), a decrease in “active protoplasm”, etc.

A reduction in “active protoplasm” can be clearly measured as the degree of sclerosis and calcium accumulation in tissues, as a decrease in tissue respiration and the level of protein and DNA synthesis, as well as by the content of total and intracellular water and by the level of bound water – the degree of hydration of molecules, etc.

Thus, it can be seen that the general concepts of entropy as a very abstract indicator directly result in a whole series of manifestations, the meaning of which age changes can be clearly understood only taking into account the theoretical concepts of the essence, meaning and general cause of the aging phenomenon.

Repair of both inanimate and living systems is possible and really happens in a unique way – by replacing old structures with new ones. In organisms, all levels of their organization are updated: at the molecular level (metabolism); at the intracellular level, subcellular structures; at the level of cell populations – cell division; at the level of supra-cellular populations (nephrons, alveoli, etc.); at the level of regeneration of organs and tissues (regeneration itself – axolotl tail, etc.).

The higher the level of structure and organization, the less the possibility of full recovery. There are completely non-renewable (except for metabolism) organisms, for example, Drosophila, which, being postmitotic organisms, do not have dividing cells, their lifespan is determined and very small, aging as a process is expressed and occurs entirely in stochastic whose type is random cell death and supra-cellular structures. In contrast, there are fully renewed organisms: the hydra has no non-renewable cells, their aging is not pronounced, and the life expectancy is not determined.

The first mathematical model of aging was created almost 200 years ago by B. Gompertz (1825) and still most accurately describes the age dynamics of human mortality and, apparently, of most other organisms. As a specialist in life insurance, Gompertz theoretically derived the practically necessary formula for increasing his mortality rate with age, which until now has been the most common quantitative description of aging itself.

Mortality, as “quantitative characterization of the inability to resist destruction,” can now be viewed as the reciprocal of vitality – the ability to withstand the totality of destructive processes.

A simple assumption about the stochasticity of the aging process is enough: the viability over time decreases in proportion to itself at each time point ( formula 2 ) in order to obtain the basic law of aging: mortality increases with age by the exponent ( formula 3 ). Such a nonspecific increase in the body’s vulnerability to all influences with age is called aging itself.

d X / d t = – k X, (2)

where k is a coefficient, X is viability, t is time.

Considering the mortality ( μ ) as an inverse viability value ( μ = 1 / X ), the basic formula (3) is obtained from formula (2) aging (B. Gompertz and W. Makekem) – with age, the overall mortality increases exponentially:

μ = Ro exp (α t) + A, (3)

where Ro is the initial mortality rate, α is the rate of increase in mortality, A is the coefficient characterizing the contribution of external influences to mortality, the effect of which weakly depends on age.

The approach to writing formula is now theoretically clear: it is an elementary differential equation that describes, for example, radioactive decay in physics and other simple probabilistic processes. The essence of the phenomenon lies in the fact that at each moment in time the state change does not depend on the prehistory, but only on the present state of the system.

The general mechanisms of such processes are also clear – these are principally probabilistic regularities associated with the ultimate stability of any elements delimited from the external environment; then a complex organism consisting of such elementary units can only lose them over time. The main issue is then the nature of such “elementary units of life.”

Gomperz himself noted the similarity of the curves of changes in mortality and entropy, and V. Perks (1932) directly wrote that “the inability to resist destruction has the same nature as energy dissipation” (that is, aging is equivalent to an increase in entropy, which serves as a measure of disorder any system); A. Comfort (1967) writes that viability can be reduced to a rather specific, though not material, substrate – information in cells, which is “just biological energy”.