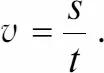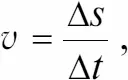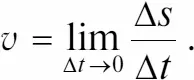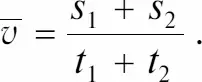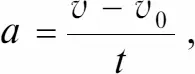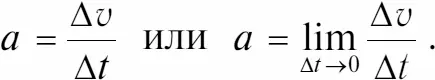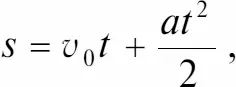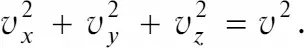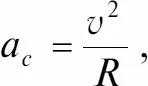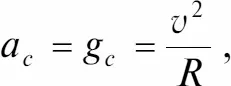Татьяна Гаева - Естествознание

При движении с постоянной скоростью v

где s – расстояние, пройденное за время t; отсюда значение скорости определяется как

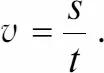
Теперь рассмотрим движение тела со скоростью, которая меняется по величине, но не по направлению (это поступательное движение). Тогда на небольших участках As, которые тело проходит за время At, значения мгновенной скорости определяются как

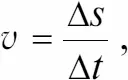
или более строго:

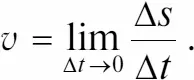
Это соотношение означает, что мгновенная скорость v есть предел отношения As/At при At, стремящемся к нулю (строгое математическое определение значения мгновенной скорости).

Если тело движется на отрезке пути s 1 в течение времени t 1 с одной скоростью, а на отрезке пути s 2 в течение времени t 2 с другой скоростью, то средняя скорость v на всем пути:

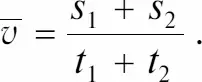
Постоянное ускорение определяется как

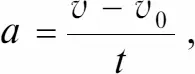
где v – v 0 – приращение скорости за время t.

Мгновенное ускорение:

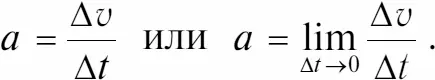
Путь при равноускоренном движении:

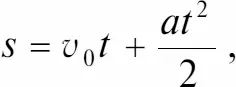
где v 0 – скорость тела в начальный момент времени.

На практике нужно знать не только значение, но и направление скорости в пространстве, например, чтобы описать движение (траекторию) автомобиля, самолета или космического корабля. Любая физическая величина, которая не будет полностью определена, если задать только ее значение и не указать, в какую сторону она направлена, является вектором.

Скорость – это вектор.Если разложить вектор скорости v при движении тела в пространстве по осям декартовой системы координат, то мы получим ее составляющие v x , v, v z . Они связаны с полной скоростью v соотношением

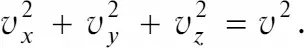
Следует отметить, что векторную природу имеет ускорение a, а также многие величины, которые мы будем использовать в дальнейшем изложении: сила F, импульс p и другие. Во всех случаях векторные величины отмечаются стрелкой «->», помещенной над буквенным обозначением величины. Значение самой величины (ее абсолютная величина) обозначается просто буквой, например, a – значение ускорения.

Рассмотрим равномерное движение тела по окружности со скоростью v. При этом его ускорение, оставаясь перпендикулярным скорости в любой момент времени, направлено к центру окружности. Можно показать, что значение ускорения тела a c , которое в данном случае называется центростремительным, определяется по формуле

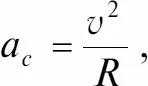
где R – радиус окружности. Следует отметить, что центростремительное ускорение меняет только направление вектора скорости, не влияя на его величину; ускорение a c направлено по радиусу окружности к ее центру.

Пример.Определение первой космической скорости.

Любое тело, движущееся по круговой орбите вокруг Земли, должно иметь ускорение a c =v 2/R , направленное к центру нашей планеты.

Поскольку на тело в этом случае действует только сила земного притяжения (т. е. сила тяжести), то можно записать

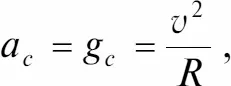
где g c – ускорение свободного падения – 9,8 м/с 2.

Тогда v c =qR.

Если считать, что R ≈ 6500 км (расстояние до центра Земли), то вычисление первой космической скорости дает значение v c = 8 км/c. Если разделить длину орбиты на скорость спутника, то получим время одного оборота спутника вокруг Земли. Длина орбиты низколетящего спутника близка к длине экватора Земли t = 40 000 км/8 км/c = 5000 c = 83 мин