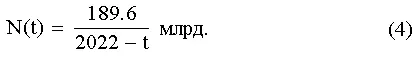Анатолий Молчанов - Население Земли как растущая иерархическая сеть II

Начало 4-го исторического периода: -31×(39,75 ± 0,25) + (1982 ± 2) = 750 ± 10

Начало 5-го исторического периода: -15×(39,75 ± 0,25) + (1982 ± 2) = 1386 ± 6

Начало 6-го исторического периода: -7×(39,75 ± 0,25) + (1982 ± 2) = 1704 ± 4

Начало 7-го исторического периода: -3×(39,75 ± 0,25) + (1982 ± 2) = 1863 ± 3

Начало 8-го исторического периода: -1×(39,75 ±0,25) + (1982 ± 2) = 1942 ± 2,25

Начало глобального демографического перехода: 1982 ± 2

Дата исторической сингулярности (сингулярности Дьяконова – Капицы): 2022 ± 2 год. Столь высокая точность для важных дат мировой истории и демографии получена благодаря большой точности, с которой была определена постоянная времени Капицы.

Точнее, эта дата лежит в интервале 1982 ± 2 года. Но имеет ли она какое-то историческое значение? Перечислим аргументы, говорящие о том, что это так:

1.1982 год отстоит от сингулярности Дьяконова – Капицы ровно на один цикл исторического времени 2022 − 40 = 1982. В соответствии с предложенным здесь простым правилом определения границ главных исторических периодов, именно в этот момент времени завершился последний, восьмой период. После чего исторический процесс перестает быть циклическим и наступает новая историческая эпоха.

2.Именно в это время завершается четвертый экономический цикл Кондратьева 1929–33 гг. – 1973–81 гг. Циклы Кондратьева являются, видимо, главными историческими циклами, задающими основной ритм мировому экономическому и историческому процессу.

3.Демографический переход, как считается, начался в шестидесятых годах двадцатого столетия. В это время относительная скорость роста численности населения мира достигла максимума и начался ее спад. Такое задание времени начала перехода соответствует определению мультипликатора Шене и является достаточно условным. Построим в одних координатных осях гиперболу (4) и интерполяцию демографических данных за 1960–1990 гг:

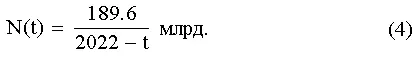
Рис 1. Закон гиперболического роста населения мира.

Гипербола (4) – лучше всего соответствует работе Фёрстера, исследованиям С.П. Капицы, работе Мак-Эведи, Джоунса и Кремера, данным Остина и Брауэра, а также и нашей теории: см. главу «Константы Капицы».

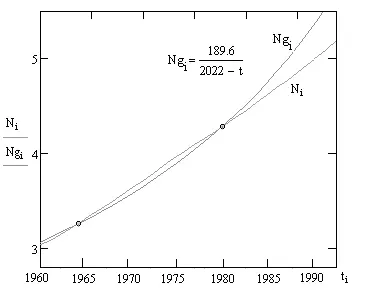
Рис 2. Гипербола (4) и интерполяция демографических данных за 1960–1990 гг.

В ~1965 году относительный мировой прирост населения мира достиг своего абсолютного максимума за всю историю роста и начался его спад. После прохождения этой точки перегиба действительная кривая роста оказалась выше эмпирической гиперболы Фёрстера. Что выглядит довольно странно – и на это обращают внимание критики работы Фёрстера и его коллег – поскольку с окончанием эры гиперболического роста она должна была отклониться от гиперболы вниз. [39] Такой подъем на завершающей стадии последнего исторического цикла подтверждает нашу теорию, согласно которой численность носителей должна соответствовать теоретической гиперболе лишь в приоритетных точках своего роста.

Так как надолго «обогнать» гиперболу невозможно, эти кривые должны были в обязательном порядке еще раз пересечься, что и произошло в 1982 году. Поскольку точка пересечения эмпирической гиперболы (4) с графиком интерполяции демографических данных (t = 1982, N = k·4,3 млрд) – последняя точка, которая принадлежит гиперболе и соответствует демографическим данным, то именно 1982 год можно с достаточным основанием считать моментом окончания гиперболического роста и началом демографического перехода.

Согласно теории Капицы, дата начала перехода – 1965 год, при этом он занимает два цикла характерного времени; момент завершения первого цикла – 2007 год, конец второго – 2049-й. Если же за момент начала перехода взять 1982 год (а именно на этот момент времени приходится завершение последнего, восьмого исторического периода), то, во-первых, подтверждается связь мирового исторического и демографического процесса и, во-вторых, конец первого цикла перехода совпадает с сингулярностью Дьяконова – Капицы, приходящейся на 2022 год.

Такие «совпадения» явно выигрывают в сравнении с безликими 1965-м и 2007 годами у С.П. Капицы, ведь все три даты: начало перехода, а также конец первого и второго его цикла имеют, по-видимому, важное историческое значение, хотя смысл его пока и неясен.