Алексей Молчанов - Системное программное обеспечение. Лабораторный практикум

Цифры ведут в состояние, соответствующее входной константе, – D. Открывающая фигурная скобка ведет в состояние C, которое соответствует обнаружению комментария – из этого состояния КА выходит, только если получит на вход закрывающую фигурную скобку. Еще одно состояние – G – соответствует лексеме «знак присваивания». В него КА переходит, получив на вход двоеточие, и ожидает в этом состоянии символа «равенство».

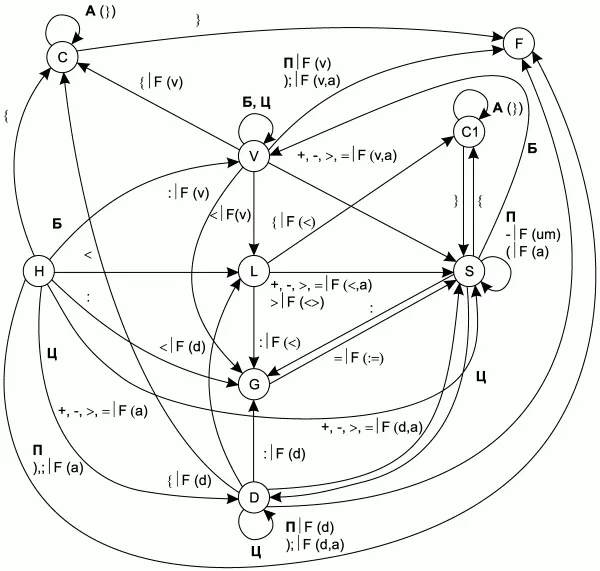
Рис. 5.1. Граф переходов сокращенного КА (без учета ключевых слов).

Знаки арифметических операций («+» и «—»), знаки операций сравнения («<.», «.>» и «=.»), открывающая круглая скобка, а также последние символы ключевых слов переводят КА в состояние S, которое отличается от начального состояния тем, что в этом состоянии КА воспринимает символ «—» как знак унарной операции отрицания, а не как знак операции вычитания. Если в состоянии S на вход КА поступает открывающая фигурная скобка, то он переходит в состояние C1 (а не в состояние C), из которого по закрывающей фигурной скобке опять возвращается в состояние S.

В еще одно состояние – состояние L – КА переходит, когда на его вход поступает знак «<.». В состоянии L автомат проверяет, является ли знак «<.» началом лексемы «<>» («неравно») или же это отдельная лексема «<.» («меньше»).

Состояние H – начальное состояние КА, а состояния F и S – его конечные состояния. Поскольку КА работает с непрерывным потоком лексем, перейдя в конечное состояние H, он тут же должен возвращаться в начальное состояние, чтобы распознавать очередную лексему. Поэтому в моделирующей программе два состояния (H и F) можно объединить в одно.

В функцию переходов КА не входит состояние «ошибка», чтобы не загромождать ее. В это состояние КА переходит всегда, когда получает на вход символ, по которому нет переходов из текущего состояния.

Видно, что граф переходов для данного КА будет слишком громоздким, чтобы его можно было наглядно представить на рисунке. Граф переходов сокращенного КА (без учета распознавания ключевых слов) представлен на рис. 5.1.

Реализация данного КА выполнена аналогично реализации КА, построенного в лабораторной работе № 2. Для описания структур данных лексем, которые не зависят от входного языка, используется модуль LexElem, который был создан при выполнении лабораторной работы № 2 (листинг П3.4, приложение 3). Типы допустимых лексем описаны в модуле LexType (листинг П3.3, приложение 3), а функционирование автомата моделируется в модуле LexAuto (листинг П3.5, приложение 3).

Для построения синтаксического анализатора будем использовать анализатор на основе грамматик операторного предшествования. Этот анализатор является линейным распознавателем (время анализа линейно зависит от длины входной цепочки), для него существует простой и эффективный алгоритм построения распознавателя на основе матрицы предшествования [1–3, 7]. К тому же алгоритм «сдвиг-свертка» для данного типа анализатора был разработан при выполнении лабораторной работы № 3, а поскольку он не зависит от входного языка, он может быть без модификаций использован в данной работе.

Для построения анализатора на основе грамматики операторного предшествования необходимо построить матрицу операторного предшествования (порядок ее построения был детально рассмотрен при выполнении лабораторной работы № 3).

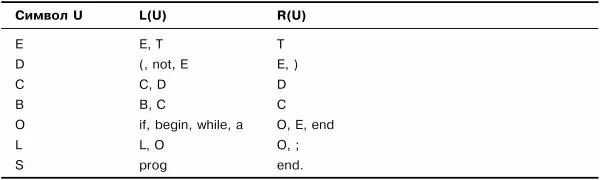
Построим множества крайних левых и крайних правых символов грамматики G. На первом шаге получим множества, приведенные в табл. 5.3.

После завершения построения мы получим множества, представленные в табл. 5.4 (детальное построение множеств крайних левых и крайних правых символов описано при выполнении лабораторной работы № 3).

После этого необходимо построить множества крайних левых и крайних правых терминальных символов. На первом шаге возьмем все крайние левые и крайние правые терминальные символы из правил грамматики G. Получим множества, представленные в табл. 5.5.