У Клоксин - ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ ПРОЛОГ

Мы можем использовать дизъюнкцию в любом месте, где может быть использовано любое другое целевое утверждение на Прологе. Однако целесообразно использовать дополнительные скобки, чтобы избежать недоразумений, касающихся взаимодействия операторов ';' и ','. Обычно мы можем избежать применения дизъюнкции путем использования нескольких фактов и правил, содержащих, возможно, определения некоторых дополнительных предикатов. Например, приведенный выше пример в точности эквивалентен следующему:

человек(адам).

человек(ева).

человек(Х):- мать(Х,Y).

Этот вариант более традиционен и, возможно, проще для чтения. Для многих Пролог-систем он может быть более эффективным по сравнению с использованием ';'.

Результатом отсечения является невозможность изменить выбор альтернатив, обусловленных наличием дизъюнкций, сделанный с момента сопоставления с правилом, содержащим отсечение (см. гл. 4). Вследствие этого имеется ряд случаев, когда программа, содержащая отсечения, не может быть преобразована в обычную программу без использования дизъюнкций. Однако в общем случае не рекомендуется чрезмерно часто использовать ';'. В качестве предостережения отсылаем вас к гл. 8, где показано, как необдуманное использование ';' затрудняет понимание программ.

Предполагается, что Xконкретизирован термом, который может быть интерпретирован как целевое утверждение. Целевое утверждение саll(X)считается согласованным, если попытка доказать согласованность Xзавершается успехом. Целевое утверждение call(X)не согласуется с базой данных, если попытка доказать согласованность Xзаканчивается неудачей. На первый взгляд этот предикат может показаться излишним, поскольку, естественно, возникает вопрос: почему аргумент callне может быть записан непосредственно как целевое утверждение? Например, целевое утверждение

…, саll(принадлежит(а,Х)),…

всегда может быть заменено следующим:

…, принадлежит(a,X),…

Однако если мы создаем целевые утверждения, используя предикат '=..' или ему подобные, то возможны обращения к целевым утверждениям, функторы которых неизвестны на момент ввода программы в Пролог-систему. Так, например, в определении предиката consultв разд. 7.13 нам надо иметь возможность рассматривать любой терм, прочитанный после ?-, как целевое утверждение. Предполагая, что Р, Хи Yконкретизированы функтором и аргументами соответственно, можно использовать callследующим образом:

…, Z =… [P,X,Y], call(Z),…

Последний фрагмент программы можно рассматривать как способ выражения обращения к целевому утверждению следующего вида:

…, P(X,Y),…

которое в рамках стандартной версии Пролога, рассматриваемой в этой книге, синтаксически некорректно. Однако некоторые версии языка Пролог допускают использование переменной в качестве функтора целевого утверждения.

Предполагается, что Xконкретизирован термом, который может быть интерпретирован как целевое утверждение. Целевое утверждение not(X)считается согласованным с базой данных, если попытка доказать согласованность Xзаканчивается неудачей. Целевое утверждение not(X)считается несогласованным, если попытка доказать согласованность X успешно завершается. В этом плане предикат notочень похож на call,за тем исключением, что согласованность или несогласованность аргумента, рассматриваемого как целевое утверждение, приводит к противоположному результату.

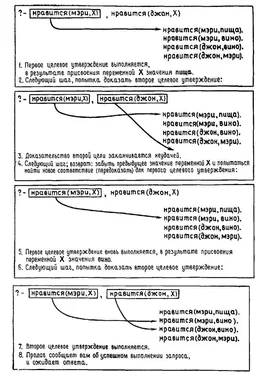
Чем отличаются следующие два вопроса?

/* 1 */?- принадлежит(Х,[а,b,с]), write(X).

/* 2 */?- not(not(принадлежит(Х,[а,b,с]))), write(X).

Может показаться, что между ними нет никакой разницы, так как в запросе 2 принадлежит(Х,[а,b,с,])согласуется, поэтому not(принадлежит(Х,[а,b,с,]))не согласуется и not(not(принадлежит(Х,[а,b,с])))согласуется. Это правильно лишь отчасти. В результате первого вопроса будет напечатан атом ' а', а в результате второго – неконкретизированная переменная. Рассмотрим, что происходит при попытке доказать согласованность первого целевого утверждения из второго вопроса:

1. Целевое утверждение принадлежитсогласуется, и Xконкретизируется значением а.

2 Предпринимается попытка доказать согласованность первого целевого утверждения not,которая заканчивается неудачей, так как целевое утверждение принадлежит,являющееся его аргументом, согласуется с базой данных. Теперь вспомним, что, когда целевое утверждение не согласуется, все конкретизированные переменные, такие как Xв нашем примере, должны теперь «забыть», что они обозначали до сих пор. Следовательно, Xстановится неконкретизированной.