У Клоксин - ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ ПРОЛОГ

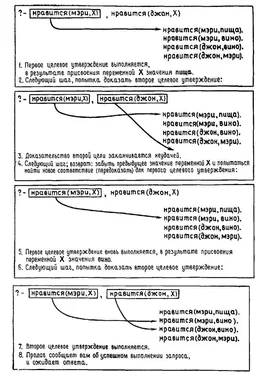
Давайте посмотрим, как все это выглядит на языке диаграмм. Если мы обратимся к предикату сумма(1,X)в следующем контексте:

выполнить:- сумма(1,X), foo(apples)

?-выполнить.

и для цели foo(apples)нет сопоставления, то к моменту, когда обнаружится несогласованность foo(apples)с базой данных, результат работы Пролога будет иметь вид, как показано на рис. 4.6. Если Пролог попытается найти новые сопоставления для целевых утверждений, просматривая их в обратном порядке, то обнаружится, что рассмотренные выше два альтернативных целевых утверждения не могут быть пересмотрены, так как они исключены из цепочки доказательства. Следовательно, наиболее верный путь – не пытаться найти другое сопоставление для предиката сумма(1,X).

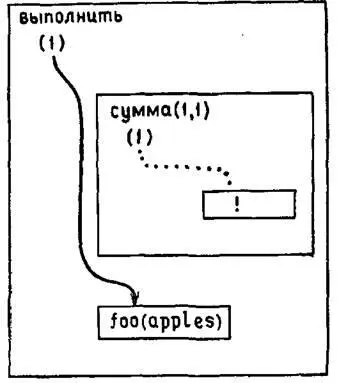
Рис. 4.6.

Упражнение 4.1.Что произойдет в процессе возврата при попытке найти новое сопоставление для целевогоутверждения сумма,если из первого правила для предиката суммаудалить отсечение? Какие альтернативные результаты будут получены (если вообще они будут возможны) и почему?

Последний пример показал, как можно использовать отсечение для того, чтобы сделать поведение Пролога чувствительным к случаю, когда мы не можем выделить все возможные случаи путем перечисления образцов в заголовках правил. Более типичная ситуация, в которой мы не можем указать структуру заголовков правил для выполнения сопоставления, возникает, если мы хотим ввести дополнительные условия в виде целевых утверждений Пролога, позволяющих в процессе согласования с базой данных выбрать соответствующие правила. Рассмотрим следующий альтернативный вариант решения последнего примера:

сумма(N,1):- N =‹ 1,!.

cyммa(N,R):- N1 is N-1, сумма(N1,R1), R is Rl+N

В этом случае указывается, что первое правило следует выбрать, когда заданное количество суммируемых чисел меньше или равно единице. Такое определение правила немного лучше, чем предыдущее, потому что соответствующая ему программа даст ответ (вместо того чтобы выполняться бесконечно), если в качестве первого аргумента будет задан 0или отрицательное число. Если условие первого правила выполняется, то сразу же выдается результат 1и не требуется прибегать к рекурсивному порождению целевых утверждений. Второе правило следует попытаться использовать лишь в случае, когда это условие не выполняется. Мы должны указать Прологу, что если уже обнаружено, что N = ‹ 1, то не следует возвращаться к пересмотру выбора правила. Это как раз и достигается с помощью отсечения.

Общий принцип заключается в том, что использование механизма отсечения для указания Прологу на ситуации, когда он выбрал единственно правильное правило, может быть заменено использованием предиката not.Это встроенный предикат Пролога, т. е. определение этого предиката заранее известно Пролог-системе. Поэтому его можно использовать, не выписывая каждый раз его определение (более полно встроенные предикаты описываются в гл. 6). Предикат notопределен таким образом, что целевое утверждение not(X)истинно, только если X, рассматриваемое как целевое утверждение, не согласуется с базой данных. Таким образом, not(X)означает, что X недоказуемо как целевое утверждение Пролога, т. е. не согласовано с базой данных. В качестве примера использования notвместо отсечения перепишем два варианта определения предиката суммаследующим образом:

сумма(1,1).

cyммa(N,R):- not(N = 1), N1 is N-1, cyммa(N1,R1),R is N1 + R1.

или

сумма(N,1):- N =‹1.

сумма(N,R):- not(N=‹l), N1 is N-1, сумма(N1,R1 ), R is N1 + R1.

В действительности в Прологе имеются другие удобные встроенные предикаты, которые могут заменить оба из приведенных вхождений предиката not.Например, можно заменить not(N=1)на N\=1,a not(N=‹ 1)на N›1.В общем случае это можно сделать не со всеми возможными условиями.

Использование предиката notвместо отсечения свойственно для хорошего стиля программирования. Это связано с тем, что программы, содержащие отсечения, как правило, более трудны для чтения, чем программы, не содержащие их. Если удается локализовать все вхождения отсечения и заменить их с помощью предиката not, то программа станет более понятной. Однако определение not предполагает попытку доказать, что заданное целевое утверждение согласуется с базой данных. Поэтому если мы имеем программу, в общем виде представимую как