Иван Братко - Программирование на языке Пролог для искусственного интеллекта

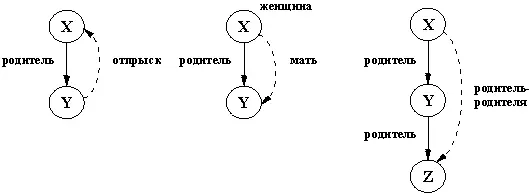
Рис. 1.3. Графы отношений родительродителя, матьи отпрыск, определенных через другие отношения.

Такие отношения как родитель, отпрыски матьможно изобразить в виде диаграмм, приведенных на рис. 1.3. Они нарисованы с учетом следующих соглашений. Вершины графа соответствуют объектам, т.е. аргументам отношений. Дуги между вершинами соответствуют бинарным (двуместным) отношениям. Дуги направлены от первого аргумента к второму. Унарные отношения на диаграмме изображаются просто пометкой соответствующих объектов именем отношения. Отношения, определяемые через другие отношения, представлены штриховыми дугами. Таким образом, любую диаграмму следует понимать так: если выполнены отношения, изображенные сплошными дугами, тогда и отношение, изображенное штриховой дугой, тоже выполнено. В соответствии с рис. 1.3, отношение родительродителяможно сразу записать на Прологе:

родительродителя( X, Z) :- родитель( X, Y),

родитель( Y, Z).

Здесь уместно сделать несколько замечаний о внешнем виде нашей программы. Пролог дает почти полную свободу расположения текста на листе. Так что можно вставлять пробелы и переходить к новой строке в любом месте текста по вкусу. Вообще мы хотим сделать так, чтобы наша программа имела красивый и аккуратный вид, а самое главное, легко читалась. Для этого мы часто будем помещать голову предложения и каждую цель на отдельной строке. При этом цели мы будем писать с отступом, чтобы сделать разницу между головой и целями более заметной. Например, правило родительродителяв соответствии с этими соглашениями запишется так:

родительродителя( X, Z) :-

родитель( X, Y),

родитель( Y, Z).

На рис. 1.4 показано отношение сестра:

Для любых X и Y

X является сестрой Y, если

(1) у X и Y есть общий родитель, и

(2) X — женщина.

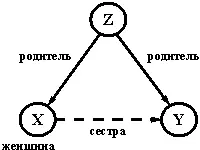
Рис. 1.4. Определение отношения сестра.

Граф на рис. 1.4 можно перевести на Пролог так:

сестра( X, Y) :-

родитель( Z, X),

родитель( Z, Y),

женщина( X).

Обратите внимание на способ, с помощью которого выражается требование "у X и Y есть общий родитель". Была использована следующая логическая формулировка: "некоторый Z должен быть родителем X и этот же самый Z должен быть родителем Y". По-другому, менее красиво, можно было бы сказать так: "Z1 - родитель X, Z2 - родитель Y и Z1 равен Z2".

Теперь можно спросить:

?- сестра( энн, пат).

Как и ожидается, ответ будет " yes" (да) (см. рис. 1.1). Мы могли бы заключить отсюда, что определенное нами отношение сестраработает правильно. Тем не менее в нашей программе есть маленькое упущение, которое обнаружится, если задать вопрос: "Кто является сестрой Пат?"

?- сестра( X, пат).

Система найдет два ответа, один из которых может показаться неожиданным:

X = энн;

X = пат

Получается, что Пат — сестра себе самой?! Наверное, когда мы определяли отношение сестра, мы не имели этого ввиду. Однако ответ Пролога совершенно логичен, поскольку он руководствовался нашим правилом, а это правило ничего не говорит о том, что, если X — сестра Y, то X и Y не должны совпадать. Пролог (с полным правом) считает, что X и Y могут быть одним и тем же объектом и в качестве следствия из этого делает вывод, что любая женщина, имеющая родителя, является сестрой самой себе.

Чтобы исправить наше правило о сестрах, его нужно дополнить утверждением, что X и Y должны различаться. В следующих главах мы увидим, как это можно сделать, в данный же момент мы предположим, что отношение различныуже известно пролог-системе и что цель

различны( X, Y)

достигается тогда и только тогда, когда X и Y не равны. Усовершенствованное правило для отношения сестрапримет тогда следующий вид:

сестра( X, Y) :-

родитель( Z, X),

родители( Z, Y),

женщина( X),

различны( X, Y).

Некоторые важные моменты этого раздела:

• Пролог-программы можно расширять, добавляя в них новые предложения.

• Прологовские предложения бывают трех типов: факты , правила и вопросы .

• Факты содержат утверждения, которые являются всегда, безусловно верными.