Иван Братко - Программирование на языке Пролог для искусственного интеллекта

% бананом, находясь в состоянии Состояние

можетзавладеть( состояние( -, -, -, имеет) ).

% может 1: обезьяна уже его имеет

можетзавладеть( Состояние1) :-

% может 2: Сделать что-нибудь, чтобы завладеть им

ход( Состояние1, Ход, Состояние2),

% сделать что-нибудь

можетзавладеть( Состояние2).

% теперь может завладеть

Рис. 2.14. Программа для задачи об обезьяне и банане.

Для ответа на наш вопрос системе пришлось сделать лишь один возврат. Верная последовательность ходов была найдена почти сразу. Причина такой эффективности программы кроется в том порядке, в котором в ней расположены предложения, касающиеся отношения ход. В нашем случае этот порядок (к счастью) оказался весьма подходящим. Однако возможен и менее удачный порядок. По правилам игры обезьяна могла бы с легкостью ходить туда-сюда, даже не касаясь ящика, или бесцельно двигать ящик в разные стороны. Как будет видно из следующего раздела, более тщательное исследование обнаруживает, что порядок предложений в нашей программе является, на самом деле, критическим моментом для успешного решения задачи.

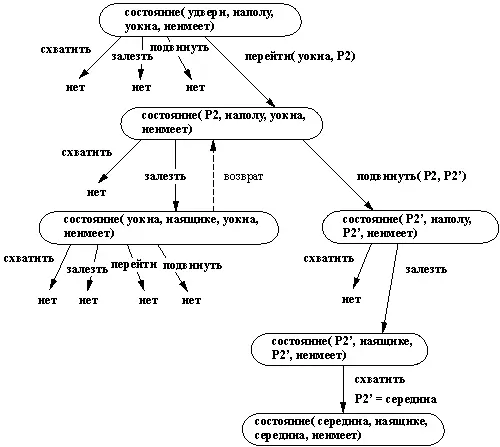
Рис. 2.15. Поиск банана обезьяной. Перебор начинается в верхнем узле и распространяется вниз, как показано. Альтернативные ходы перебираются слева направо. Возврат произошел только один раз.

Рассмотрим следующее предложение:

p :- p.

В нем говорится: "p истинно, если p истинно". С точки зрения декларативного смысла это совершенно корректно, однако в процедурном смысле оно бесполезно. Более того, для пролог-системы такое предложение может породить серьезную проблему. Рассмотрим вопрос:

?- p.

При использовании вышеприведенного предложения цель p будет заменена на ту же самую цель p; она в свою очередь будет заменена снова на p и т.д. В этом случае система войдет в бесконечный цикл, не замечая, что никакого продвижения в вычислениях не происходит.

Данный пример демонстрирует простой способ ввести пролог-систему в бесконечный цикл. Однако подобное зацикливание могло встретиться и в некоторых наших предыдущих программах, если бы мы изменили порядок предложений, или же порядок целей в них. Будет полезно рассмотреть несколько примеров.

В программе об обезьяне и банане предложения, касающиеся отношения ход, были упорядочены следующим образом: схватить, залезть, подвинуть, перейти (возможно, для полноты следует добавить еще "слезть"). В этих предложениях говорится, что можно схватить, можно залезть и т.д. В соответствии с процедурной семантикой Пролога порядок предложений указывает на то, что обезьяна предпочитает схватывание залезанию, залезание — передвиганию и т.д. Такой порядок предпочтений на самом деле помогает обезьяне решить задачу. Но что могло случиться. если бы этот порядок был другим? Предположим, что предложение с "перейти" оказалось бы первым. Процесс вычисления нашей исходной цели из предыдущего раздела

?- можетзавладеть( состояние( удвери, наполу, уокна, неимеет) ).

протекал бы на этот раз так. Первые четыре списка целей (с соответствующим образом переименованными переменными) остались бы такими же, как и раньше:

(1) можетзавладеть( состояние( удвери, наполу, уокна, неимеет) ).

Применение второго предложения из можетзавладеть("может2") породило бы

(2) ход( состояние( удвери, наполу, уокна, неимеет), М', S2'),

можетзавладеть( S2')

С помощью хода перейти( уокна, Р2')получилось бы

(3) можетзавладеть( состояние( Р2', наполу, уокна, неимеет) )

Повторное использование предложения "может2" превратило бы список целей в

(4) ход( состояние(Р2', наполу, уокна, неимеет), М'', S2''),

можетзавладеть( S2'')

С этого момента начались бы отличия. Первым предложением, голова которого сопоставима с первой целью из этого списка, было бы теперь "перейти" (а не "залезть", как раньше). Конкретизация стала бы следующей:

S2'' = состояние( Р2'', наполу, уокна, неимеет).

Поэтому список целей стал бы таким:

(5) можетзавладеть( состояние( Р2'', наполу, уокна, неимеет) )

Применение предложения "может2" дало бы

(6) ход( cocтояниe( P2'', наполу, yoкнa, неимeeт), M''', S2'''),