Иван Братко - Программирование на языке Пролог для искусственного интеллекта

11.2. Напишите процедуру поиска в глубину, сочетающую в себе обнаружение циклов с ограничением глубины, используя рис. 11.7 и 11.8.

11.3. Проведите эксперимент по применению программы поиска в глубину к задаче планирования в "мире кубиков" (рис. 11.1).

11.4. Напишите процедуру

отобр( Ситуация)

для отображения состояния задачи "перестановки кубиков". Пусть Ситуация — это список столбиков, а столбик, в свою очередь, — список кубиков. Цель

отобр( [ [a], [e, d], [с, b] ] )

должна отпечатать соответствующую ситуацию, например так:

e с

a d b

==============

В противоположность поиску в глубину стратегия поиска в ширину предусматривает переход в первую очередь к вершинам, ближайший к стартовой вершине. В результате процесс поиска имеет тенденцию развиваться более в ширину, чем в глубину, что иллюстрирует рис. 11.9.

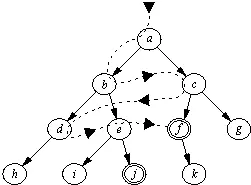
Рис. 11.9.Простое пространство состояний: а — стартовая вершина, f и j — целевые вершины. Применение стратегии поиска в ширину дает следующий порядок прохода по вершинам: а, b, c, d, e, f. Более короткое решение [a, c, f]найдено раньше, чем более длинное [а, b, e, j]

Поиск в ширину программируется не так легко, как поиск в глубину. Причина состоят в том, что нам приходится сохранять все множество альтернативных вершин-кандидатов, а не только одну вершину, как при поиске в глубину. Более того, если мы желаем получить при помощи процесса поиска решающий путь, то одного множества вершин недостаточно. Поэтому мы будем хранить не множество вершин-кандидатов, а множество путей -кандидатов. Таким образом, цель

вширину( Пути, Решения)

истинна только тогда, когда существует путь из множества кандидатов Пути, который может быть продолжен вплоть до целевой вершины. Этот продолженный путь и есть Решение.

В нашей первой реализации этой идеи мы будем использовать следующее представление для множества путей-кандидатов. Само множество будет списком путей, а каждый путь - списком вершин, перечисленных в обратном порядке, т.е. головой списка будет самая последняя из порожденных вершин, а последним элементом списка будет стартовая вершина. Поиск начинается с одноэлементного множества кандидатов

[ [СтартВерш] ]

решить( Старт, Решение) :-

вширину( [ [Старт] ], Решение).

вширину( [ [Верш | Путь] | _ ], [Верш | Путь] ) :-

цель( Верш).

вширину( [ [В | Путь] | Пути], Решение ) :-

bagof( [B1, В | Путь ],

( после( В, В1), not принадлежит( В1, [В | Путь])),

НовПути),

% НовПути - ациклические продолжения пути [В | Путь]

конк( Пути, НовПути, Пути1), !,

вширину( Путь1, Решение);

вширину( Пути, Решение).

% Случай, когда у В нет преемника

Рис. 11.10. Реализации поиска в ширину.

Общие принципы поиска в ширину таковы:

Для того, чтобы выполнить поиск в ширину при заданном множестве путей-кандидатов, нужно:

• если голова первого пути — это целевая вершина, то взять этот путь в качестве решения, иначе

• удалить первый путь из множества кандидатов и породить множество всех возможных продолжений этого пути на один шаг; множество продолжений добавить в конец множества кандидатов, а затем выполнить поиск в ширину с полученным новым множеством.

решить( Старт, Решение) :-

вширь( [ [Старт] | Z ]-Z, Решение).

вширь( [ [Верш | Путь] | _ ]-_, [Верш | Путь] ) :-

цель( Верш).

вширь( [ [В | Путь] | Пути]-Z, Решение ) :-

bagof( [B1, В | Путь ],

( после( В, В1),

not принадлежит( В1, [В | Путь]) ),

Нов ),

конк( Нов, ZZ, Z), !,

вширь( Пути-ZZ, Решение);

Пути \== Z, % Множество кандидатов не пусто

вширь( Пути-Z, Решение).

Рис. 11.11. Программа поиска в ширину более эффективная, чем программа рис. 11.10. Усовершенствование основано на разностном представлении списка путей-кандидатов.

В случае примера рис.11.9 этот процесс будет развиваться следующим образом:

(1) Начинаем с начального множества кандидатов:

[ [а] ]

(2) Порождаем продолжения пути [а]:

[ [b, а], [с, а] ]

(Обратите внимание, что пути записаны в обратном порядке.)