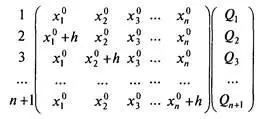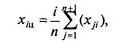В Камаев - Технологии программирования

Критерий окончания поиска, использованный Нелдером и Мидом, состоял в проверке условия среднего квадратичного отклонения функций f(x (k) i) от произвольного малого числа ε.

Химмельблау воспользовался традиционным математическим стилем для изложения описания алгоритма. Алгоритм имеет структуру вида "спагетти", что видно из схемы алгоритма, разработанной автором (рис. 5.15). Схема в виде "спагетти" — это скрытые go to, которые мы обнаруживаем в тексте программы, разработанной автором. Он же приводит графические рисунки принципа расчета точек и графический рисунок последовательности продвижения лучших точек симплекса по шагам метода при решении тестовой задачи. Затратив 11 страниц текста, приведя текст неструктурированной программы на 12 страницах, автор книги [26] так и не сумел понятно описать свой алгоритм.

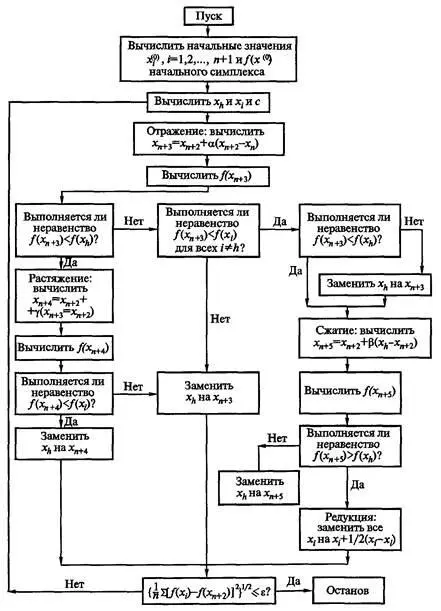
Рис. 5.15. Схема алгоритма, разработанная Д. Химмельблау

Сравните способ подачи описания алгоритма, составленный автором [22], и функциональное описание алгоритма после рефакторинга. Функциональное описание алгоритма приведено ниже.

Особенностью алгоритма является продвижение к экстремуму целым облаком пробных точек, который условно назван симплексом (деформируемым многогранником). Общее число точек в симплексе равно увеличенному на единицу числу переменных поиска. Продвижение к экстремуму не по линии от одной точки к другой, а внутри какого-то множества пробных точек обеспечило нереагирование на мелкие дефекты целевой функции и прохождение относительно "широких" оврагов.

Вводимая информация:

n — число переменных минимизируемой функции;

X 0 = (x 0 1, x 0 2…, x 0 n) — точка первого начального приближения;

h — шаг регуляризации симплекса;

ε x— погрешность нахождения экстремума по параметрам.

Работа алгоритма начинается с начальной подготовки симплекса точек. После выполнения процедур регуляризация симплекса и расчета значений целевой функции во всех точках симплекса имеет вид

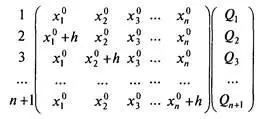
Процедура регуляризации симплекса состоит в копировании во все поля значений аргументов симплекса значения вектора X 0, и далее производятся изменения значений диагональных компонент векторов с номерами от 2 до n + 1 путем их увеличения на шаг регуляризации симплекса h.

В симплексе Q 1, Q 2, Q 3…, Q n+1— это рассчитанные значения минимизируемой функции при соответствующих по строке значениях аргументов минимизируемой функции.

Далее до выполнения условия окончания поиска осуществляются итерации (шаги) поиска. Условием окончания поиска этого метода является неудаленность от лучшей точки симплекса остальных точек симплекса более чем на e 2 x.

Каждая итерация начинается с нахождения номеров l и k, соответственно лучшей и худшей по значению функции точек симплекса. Далее осуществляется расчет точки X ц— положения центра масс всех точек симплекса за исключением наихудшей точки 1. Это позднее улучшение алгоритма. Д. Химмельблау не исключал наихудшей точки.

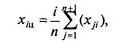
где n — количество точек в симплексе; i — номер компоненты вектора X(i = 1, 2…, n); j — номер точки в симплексе.

Считаются нулевыми значения x kjслагаемых сумм, где k — номер наихудшей точки.

При работе метода на каждой из итерации может вычисляться одна из особых пробных точек: а — точка отражения, р — точка растяжения, у — точка сжатия. Точки вычисляются по формулам:

X α = X ц+ α(X ц— X k), X β= X ц+ β(X ц— X k), X γ= X ц+ γ(X ц— X k).

Целесообразно эти похожие формулы реализовать одной функцией.

Значения коэффициентов α = 1, β = 0,5 и γ = 2 подобраны экспериментальным путем (в оригинале описания алгоритма эти значения можно выявить лишь из текста программ). Расчет точек α, β, γ целесообразно осуществлять одной процедурой с параметром в виде значений коэффициентов α, β, γ.

После расчета точки X цвычисляется пробная точка α. Далее выполняется одно из альтернативных действий.

Если Q α≤ Q 1, то выполняются действия достижения сильного успеха. Если Q 1≤ Q α< Q k, то имеется слабый успех, а точка α записывается на место k-точки. Если Q α≥ Q k, то выполняются действия отсутствия успеха. Рассчитывается X βи Q β. Далее, если Q β≤ Q k, то точка β записывается на место k-точки, иначе, если точка β хуже точки k, выполняется процедура редукции симплекса и процедура расчета значения функции в точках симплекса.