Договоримся о форме записи двоичных чисел, иначе путаницы не избежать. У программистов приняты две формы: к символам двоичного изображения добавляют либо суффикс «B» (от Binary – «двоичный»), либо маленькую двоечку. Например, число 12 в двоичной системе записывается так:
1100B или 1100b или 1100 2
А иначе эту запись можно понять как «тысяча сто» в десятичной системе.
Шестнадцатеричная система
Компьютеры никогда не жаловались на двоичную систему, она их вполне устраивает. Сетовать стали программисты, – уж очень громоздкой получалась запись сравнительно небольших чисел, например:
4005 = 111110100101 2
А если программистам несподручно, они что-нибудь придумают. Придумка была простой: двоичную запись разбили на группы по четыре двоичных цифры в каждой – тетрады (от греческого слова Tetra – «четыре»). И каждую тетраду записали в привычной для людей десятичной системе, разделяя тетрады точками. Например, десятичное число 4005 преобразили так:
4005 = 111110100101 2–> 1111.1010.0101 2–> 15.10.05
Тетрады могут содержать числа от 0 до 15 – всего получается 16 значений, потому систему назвали шестнадцатеричной. Со временем запись сделали ещё короче, заменив числа от 10 до 15 буквами латинского алфавита:
A=10
B=11
C=12
D=13
E=14
F=15
Тогда показанная выше запись преобразилась так: 15.10.05 –> FA5
Рис. 107 показывает это наглядней.
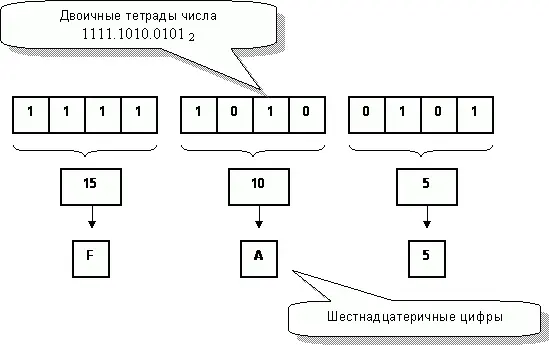
Рис.107 – Преобразование двоичного числа в шестнадцатеричное
Шестнадцатеричную запись можно спутать с десятичной, и даже принять за слово, поскольку в ней встречаются буквы. Потому для таких чисел учредили свои правила: шестнадцатеричная запись числа должна начинаться с цифры, а завершаться суффиксом «H» (от Hexadecimal, Hex – «шестнадцатеричный»). Значит, изобразить число FA5 правильней так:
0FA5H или 0FA5h
Применяют и другие формы записи шестнадцатеричных чисел. Так, в языке Си принята приставка «0x» (0xFA5), а в Паскале начинают с приставки «$» – это знак доллара ($FA5). В таких записях лидирующий ноль не требуется, но для лучшего восприятия указывают обычно две, четыре, либо восемь цифр (в зависимости от величины числа или разрядности данных), например:
12 = 0x0C = $0C <���– байт (byte)
4005 = 0x0FA5 = $0FA5 <���– слово (word)
4005 = 0x00000FA5 = $00000FA5 <���– длинное слово (longint)
Чем хороша шестнадцатеричная система? Легкостью перевода чисел в двоичную систему и обратно. После небольшой тренировки любой может сделать это в уме. При переводе в двоичную систему заменяем каждую шестнадцатеричную цифру четырьмя двоичными и «склеиваем» эти тетрады между собой. И, хотя компьютеры по-прежнему работают в двоичной системе, программисты дружно перешли на шестнадцатеричную. Вот таблица для перевода небольших чисел из одной системы в другую.
Табл. 11 – Изображения чисел в различных системах счисления
| Десятичная |
Двоичная |
16-ричная |
Десятичная |
Двоичная |
16-ричная |
| 0 |
0000 |
0 |
8 |
1000 |
8 |
| 1 |
0001 |
1 |
9 |
1001 |
9 |
| 2 |
0010 |
2 |
10 |
1010 |
A |
| 3 |
0011 |
3 |
11 |
1011 |
B |
| 4 |
0100 |
4 |
12 |
1100 |
C |
| 5 |
0101 |
5 |
13 |
1101 |
D |
| 6 |
0110 |
6 |
14 |
1110 |
E |
| 7 |
0111 |
7 |
15 |
1111 |
F |
Другие системы счисления
Итак, мы познакомились с тремя позиционными системами счислений: десятичной, двоичной и шестнадцатеричной. Существуют ли другие системы? Конечно! Во всех позиционных системах вес цифры определяется её положением в числе, сравните.
2048 = 2• 10 3+ 0• 10 2+ 4• 10 1+ 8• 10 0- десятичная;
12 = 1100 2= 1• 2 3+ 1• 2 2+ 0• 2 1+ 0• 1 0- двоичная;
4000 = $FA0 = F• 16 2+ A• 16 1+ 0• 16 0- шестнадцатеричная.
Число, на котором построена система, называют её основанием. Можно выдумать столько систем счисления, сколько существует чисел, то есть, бесконечно много. Пока нам достаточно тех, что придуманы. А если с других планет прилетят существа с семью пальцами на руках? Для них, вероятно, «родной» будет семеричная система, и мы должны быть готовы к этому!
Читать дальше












