Виктор Ерукаев - Продовольственный ритейл Дальнего Востока. Регион несетевой розницы

Так что же заставляет продовольственную розницу за пределами ДФО организовываться в торговые сети, вкладываться в строительство распределительных центров и реально управлять своими продажами, не отдавая их на откуп поставщикам?

Знание законов статистики

Рассмотрим пример с продажами одной SKU ходового товара первой необходимости. В нашем случае это будет литровая упаковка молока известной марки.

В отдельном магазине этот товар всегда есть в наличии, потому что товаровед берет его «с запасом» на всякий случай. Если этого «всякого» случая не случится – поставщик заберет просроченные остатки. Средние продажи этого молока – 25 упаковок в сутки. Но иногда продается меньше 5 упаковок (хорошая погода и все уехали на пляж), а иногда больше 40 (в соседнем кафе молоко кончилось). График вероятности суточных продаж выглядит следующим образом:

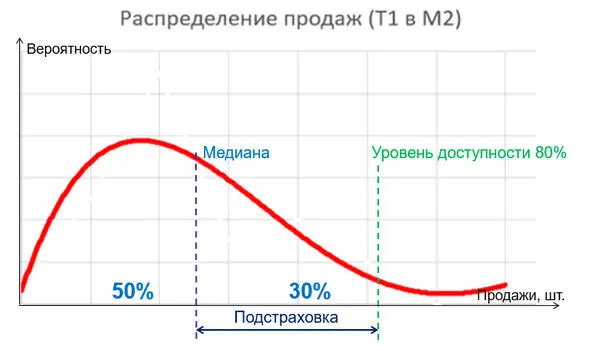
Рис. 1. Типовое распределение вероятности продаж в отдельном магазине.

Такой график показывает, что наличие в магазине 25 упаковок рассматриваемого товара позволит удовлетворить спрос на него в 50% случаев. Если мы планируем увеличить уровень доступности этого SKU до 80% (то есть покупатель найдет товар на полке в 8 случаях из 10), то нам нужно хранить уже 52 упаковки. Это типовое распределение вероятности продаж для отдельной торговой точки, и характеризуется оно наличием длинного «хвоста» справа, так как всегда будет 1—2 дня в месяц или в квартал, когда за сутки продастся 50—60 упаковок рассматриваемого SKU. В терминах логистики управления запасами для каждого отдельного магазина с независимым снабжением необходимо держать страховой запас продукта (подстраховку) в размере, превышающем среднесуточные продажи (среднесуточные продажи 25 упаковок, «подстраховка» – 27 упаковок), что позволит обеспечить хотя бы 80-процентную доступность товара для покупателя. Если бы мы поставили перед собой более высокую планку, например, обеспечить 90%-ную доступность, страховой запас для данной торговой точки пришлось бы увеличить до 65 упаковок.

Что происходит с продажами при объединении магазинов в сеть? Графически это можно изобразить следующим образом:

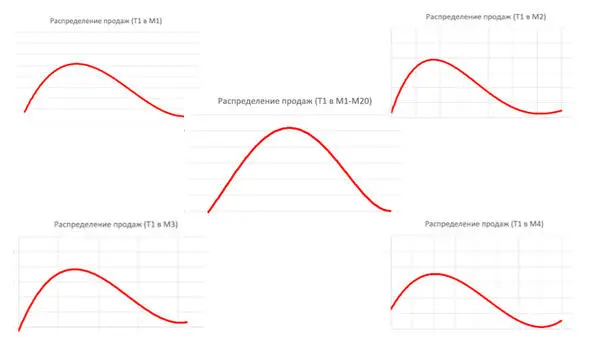
Рис. 2. Графики распределений вероятностей продаж в отдельных магазинах торговой сети и в сети в целом.

В центре – график распределения вероятности продаж в сети из 20 магазинов. Как видно, «хвоста» справа уже нет и кривая распределения стала симметричной. В действие вступила центральная предельная теорема статистики: распределение множества независимых или слабо зависимых значений склонно иметь распределение вероятностей, близкое к нормальному. Чем же хорошо для нас нормальное распределение? Прежде всего отличными возможностями математического моделирования. Посмотрим на график поближе:

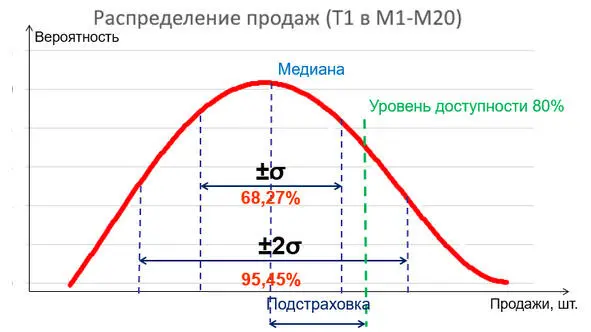
Рис. 3. Распределение вероятностей совокупных продаж в торговой сети из 20 магазинов.

Не вдаваясь в подробности описания закономерностей нормального распределения вероятностей, остановимся только на понятии среднеквадратичного отклонения, которое обозначается греческой буквой σ (сигма). Нам нужно знать, что среднеквадратичное отклонение легко считается в Exсel или в 1С и позволяет достаточно точно вычислить интервал заданной вероятности. К примеру, отклонение от среднего значения на ±σ позволяет задать интервал, в который с вероятностью 68,27% попадут наши значения продаж, а в отклонение от среднего значения на ±2σ задают интервал, в который попадут 95,45% всех наших замеренных значений продаж. То есть достаточно постоянно знать свои среднесуточные продажи, например, за последние 3 месяца и, если они укладываются в нормальный закон распределения (а это совокупные продажи не менее 20 магазинов), постоянно в автоматическом режиме вычислять среднеквадратичное отклонение, чтобы понимать, какой должна быть величина нашей «подстраховки» – страхового запаса товара – для обеспечения заданного уровня доступности товара для покупателя. В случае, если мы задаем уровень доступности 95% (для товаров повседневного спроса и для самых высокомаржинальных товаров), нам нужно держать запас товара в размере среднесуточных продаж плюс страховой запас в размере двух среднеквадратичных отклонений. И это уже математика, а не угадывание спроса на основе опыта товароведа или продавца, отбивающегося от натиска очередного торгового представителя поставщика.