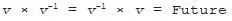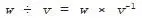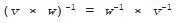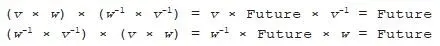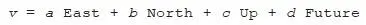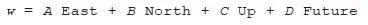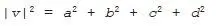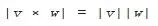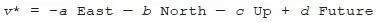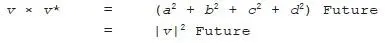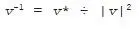Greg Egan - The Eternal Flame

Appendix 2:

Light and colors

The names of colors are translated so that the progression from “red” to “violet” implies shorter wavelengths. In the Orthogonal universe this progression is accompanied by a decrease in the light’s frequency in time. In our own universe the opposite holds: shorter wavelengths correspond to higher frequencies.

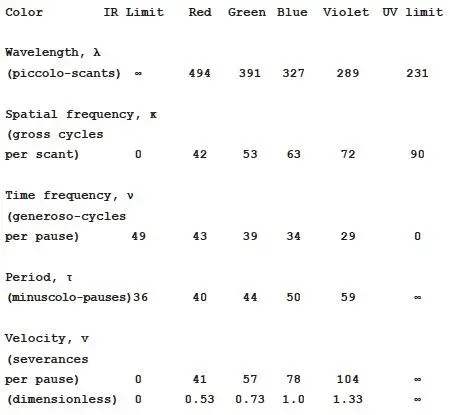
The smallest possible wavelength of light, λ min, is about 231 piccolo-scants; this is for light with an infinite velocity, at the “ultraviolet limit”. The highest possible time frequency of light, ν max, is about 49 generoso-cycles per pause; this is for stationary light, at the “infrared limit”.

Appendix 3:

Vector multiplication

and division

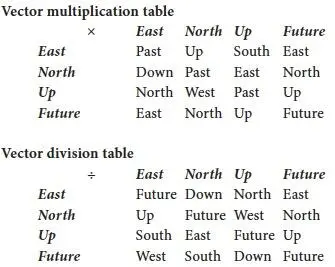
The travelers on the Peerless have developed a way of multiplying and dividing four-dimensional vectors, turning these vectors into a fully fledged number system like the more familiar real and complex numbers. In our own culture, this system is known as the quaternions; it was discovered by William Hamilton in 1843. Just as the real numbers form a one-dimensional line and the complex numbers form a two-dimensional plane, the quaternions form a four-dimensional space, making them the ideal number system for four-dimensional geometry. In our universe the distinction between time and space prevents us making full use of the quaternions, but in the Orthogonal universe the geometry of four-space and the arithmetic of the quaternions fit together seamlessly.

In the version used on the Peerless , the principal directions in the four dimensions are called East, North, Up and Future, with opposites West, South, Down and Past. The Future direction takes the role of the number one: multiplying or dividing any vector by Future leaves the original vector unchanged. Squaring any of the other three principal directions—East, North and Up—always gives Past, or minus one, so this number system contains three independent square roots of minus one, compared to the single square root of minus one, i , in the complex numbers. (Of course squaring the opposite directions—West, South and Down—also gives Past, just as in the complex numbers squaring – i also gives minus one, but these aren’t counted as independent square roots.)

Multiplication in this system is non-commutative: a × b generally isn’t the same as b × a .

Every non-zero vector v has a unique reciprocal or inverse, written v -1, which is the vector for which:

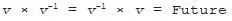
For example, East -1= West, North -1= South, Up -1= Down and Future -1= Future. In the first three cases the inverse of the vector is its opposite, but that’s not true in general.

When we divide vectors, w ÷ v is just multiplication (on the right side) by v -1:

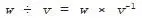
Because multiplication is non-commutative, we need to be careful with the order of vectors when we take inverses or perform division. Taking the inverse of two or more vectors multiplied together entails reversing their order :

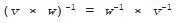
This reversal is necessary to ensure that the original vectors come together in the right sequence to give a final result of Future:

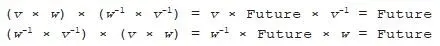
Similarly, when we divide by a product of vectors we need to reverse their order:

Although the tables only give the results for multiplying and dividing the four principal directions, the same operations can be applied to any vectors at all (with the exception that you can’t divide by the zero vector). A completely general vector can be formed by adding together various multiples of the principal directions:

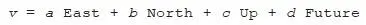
Here a , b , c and d are real numbers, and they can be positive, negative or zero. Let’s define another vector, w , using four other real numbers, A , B , C and D :

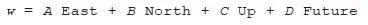
We can multiply v and w together by following the ordinary rules of algebra, taking care with the order in which we write the products of vectors:

The length of a vector can be found from the four-dimensional version of Pythagoras’s Theorem. We write the length of the vector v as | v |, and it is related to the size of its components in each direction by:

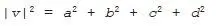
When two vectors are multiplied together, the length of the resulting vector is just the product of the lengths of the original vectors:

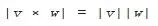
Given a vector v it’s often useful to talk about its conjugate , which we write as v * and define as the vector whose components in the three space directions are the opposite of those of v , while its component in the time direction is exactly the same as that of v :

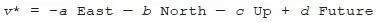
Multiplying a vector by its own conjugate gives a very simple result:

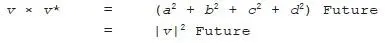
Since the direction Future acts like the number one in this system, if v has a length of one its conjugate v * will also be its inverse, v -1. If the length of v is not one, we can still find its inverse from its conjugate by dividing by the square of its length:

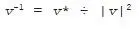
Because of this close relationship between the conjugate of a vector and its inverse , it’s not hard to see that if we take the conjugate of a product of vectors we need to reverse their order, just as we do with the inverse: