Greg Egan - The Eternal Flame

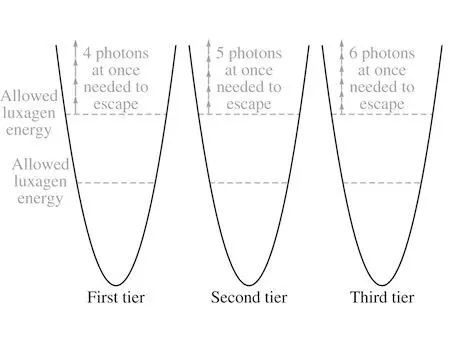
“I still don’t understand the details of the timing,” Carla confessed, “but if you don’t get to make the photons separately, one by one, there’s no reason to expect the time it takes to be proportional to the number of photons.”

“Can we quantify any of this?” Patrizia asked.

Carla said, “We could try to write an equation for the luxagen wave. Whatever we know about the luxagen’s energy, we translate into the wave’s frequency; whatever we know about the luxagen’s momentum, we translate into the wave’s spatial frequency .”

The idea seemed straightforward, but they struck a problem almost at once. Taking the rate of change of an oscillating wave multiplied it by a factor proportional to its frequency, but also shifted the wave by a quarter-cycle: at every peak of the original wave the rate of change crossed zero, heading downwards, while at every such zero of the original wave the rate of change was at a minimum, the bottom of a trough. When Yalda had devised her light equation she had been able to go one step further: the second rate of change was shifted by another quarter-cycle, putting it a half-cycle away from the original—yielding the original wave turned upside down and multiplied by the frequency squared.

Multiples of the original wave were easy to combine. The geometrical relationship Yalda had sought to express—that the sum of the squares of the wave’s frequencies in all four dimensions was a constant—could be encoded in the wave equation simply by multiplying every term in that relationship by the strength of the wave, then re-expressing the squared frequencies as second rates of change.

But with a luxagen in a solid, the relationship between its energy and momentum included its potential energy, which depended on its position in the energy valley. It was impossible to write this relationship purely in terms of the energy squared —so it was impossible to talk only of frequencies squared . To go halfway and include the frequency itself meant taking the square root of the operation that turned the wave upside down—putting the square root of minus one into the wave equation.

“It looks as if we’re stuck with complex numbers,” Carla declared. “What does that mean? That our premises are wrong?”

Patrizia seemed to share her sense of trepidation, but she wasn’t ready to give up. “Let’s follow the mathematics,” she suggested. “We should see what the final answers are before deciding whether or not it all makes sense.”

To make the calculations easier they chose a field described by a single number—albeit complex—rather than a vector like light, with its different polarizations. They also assumed that the luxagen would be moving slowly. For a parabolic energy valley—the easiest idealization to work with—it was possible to solve the equation exactly.

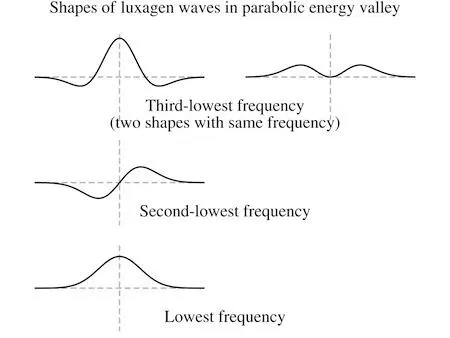
As Patrizia had guessed from the start, there was a sequence of solutions with distinct shapes. Those shapes could be described with real numbers alone, though the wave’s variation over time swept out a circle in the complex number plane with a frequency corresponding to its energy.

Some solutions shared the same energy, though that was just a consequence of the idealized shape of the valley. Carla pushed on further and managed to calculate the effect of switching to a more realistic valley, closer to the kind that was actually produced by Nereo’s force in a solid.

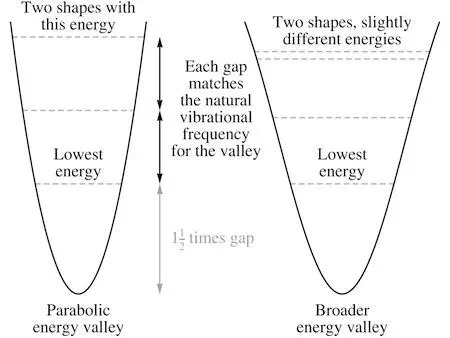
For the parabolic case all the energies were governed by the natural frequency at which a luxagen—as a particle—would be expected to vibrate in such a valley. The gaps between the allowed energies all corresponded precisely to that frequency, while the lowest energy sat one and a half times higher above the valley floor. For a more realistic valley, all the energies were reduced slightly, and the perfect agreement between the multiple higher-energy solutions broke down, splitting the idealized single energy levels into closely spaced sets.

Onesto said, “Suppose the natural frequency for the valley is greater than the maximum frequency of light. That’s the assumption at the core of the original theory of solids. But what does it mean, in your terms?”

Carla thought for a moment. “It means the energy gap exceeds the mass of a photon—so creating a single photon can never give you enough energy to jump the gap.”

“And if the valley’s not a perfect parabola,” Onesto observed, “that doesn’t really change the significance of the main energy gaps, does it? There’ll be smaller gaps as well, but if the main ones are large enough there’ll still be energy levels where you need to make more than one photon in order to rise any higher.”

“Right,” Carla said. “And if the valley is deep enough, those gaps could end up so large that you’d need to make six or seven photons to cross them.”

Patrizia turned to Carla. “Doesn’t that… solve the stability problem?”

Carla considered the question seriously. In the old way of looking at the problem, even if the walls of the energy valley were so steep that the luxagen rolled back and forth at a rate dozens of times greater than the maximum frequency of light, the tiniest deviation from a parabolic shape would introduce lower-frequency components into its motion—some of them low enough to produce light. And however feeble the radiation emitted that way, the luxagen would slowly gain energy and creep up the valley, until it finally escaped.

But that was in a world where energies could take on any value at all. In the new theory of luxagens as waves, a steep enough valley would have gaps between its energy levels that were insurmountable—and the inevitable imperfections in the shape of the valley would merely split some of those levels. As Onesto had pointed out, if the rungs of the original energy ladder were spaced sufficiently widely, adding a few extra rungs close to the originals wouldn’t suddenly make the whole thing traversable. The valley’s imperfection no longer undermined its stability.

“We still don’t know how long it takes to create a given number of photons,” Carla said cautiously. “But we do know that it takes much longer to make five than four, and a great deal longer to make six—even with the beam from a sunstone lamp to help. If we could understand what was going on there, I think we’d be getting close to explaining how some solids can be stable.”

Patrizia sketched the shapes of the first few luxagen waves on her own chest. “What happens if I add two of these solutions together—two waves with different energies? The sum will still solve the same equation… so what does the combined wave represent? Two luxagens, one with each energy?”

Carla said, “That doesn’t sound right. We found the wave equation by translating the energy-momentum relationship for a single particle. And what if I add two solutions in unequal proportions? Say, one quarter the first solution and three quarters the other?”

“Couldn’t that be… one particle with the first energy, and three with the second?” Patrizia didn’t sound too persuaded herself; she could probably see where this numbers game was heading.

“ Irrational proportions, then,” Carla replied. “Multiply the second solution by the square root of two, then add it to the first. It’s still just one particle.”