Александр Казанцев - Дар Каиссы (сборник)

Поп рассвирепел, затряс гривой: «А ежели в третий раз человек упал с колокольни и жив остался, что это такое? Ответствуй!» Тут семинарист выпрямился и отчеканил: «Привычка!» – и стал несостоявшимся попиком.

– Так вы хотите сказать, что с конем и пешкой это уже «привычка»? – вскипел Михаил Николаевич.

– Вы все хотите, чтобы я произнес «чудо»? – пытался я улыбкой успокоить его.

– Так я вам покажу нечто непривычное . В пифагорову теорему верите?

– Я кивнул.

– Неверна она тут для коневой диагонали!

– Это как же? Ее как будто тоже в Индии доказали.

И я вспомнил это доказательство.

– Совершенно верно. Как известно, Пифагор бывал в Индии и мог узнать о доказательстве, принесенном из Шамбалы.

– Опять Шамбала?

– Конечно! Все, что я рассказывал, – все из Шамбалы. Так вот! Конь! Коневая диагональ (рис. 166), проведенная через поля, по которым пройдет конь, затронет за один оборот спирали четыре поля и восемь – за два, когда квадрат будет пройден от края до края, сумма цифр при этом будет 130 + 130 = 260! И что самое интересное, если строить после трех ходов коня треугольник на его диагонали, как на гипотенузе, с катетами на сторонах квадрата, то сумма цифр гипотенузы будет просто равна сумме цифр малого катета. Вот вам и Пифагор!

– Так то сумма цифр, а не длина! Это что-то новое.

– Новое – значит непривычное. А вы говорите «привычка»!

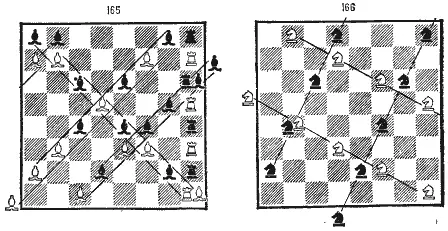
Теперь пешки! Выстроенные в ряд, они дают константу. Но если они передвинутся и две из них побьют в разные стороны, то новый ряд снова даст константу (рис. 167). Движение же центральной пешки (рис. 168) – d3-de-ed-d6-d7-d8 дает ту же сумму цифр 260.

Или черная пешка а7. Она идет по полям а6-а5-а4-аЗ-Ь2, и теперь взятие или на а1 или на с1. В одном случае сумма цифр будет 259, а в другом 261. В среднем та же константа 260, хотя пешки проходят не восемь, а лишь семь полей.

Я еще не признался, не произнес слово «чудо», но оно могло бы произойти, если бы Михаил Николаевич открыл тайну алгоритма. Но он не скрывал ее (если знал!).

Увлеченный моей фантазией, он уверял меня, что махатм сказал Рериху много больше, чем я вообразил.

Но этого не записано в дневнике.

– Тем не менее в шахматах отражены не только математические, но и биологические константы. Одно сходство слов: «шахматы» и «махатмы» чего стоит!

– Ну, это вы уж слишком!

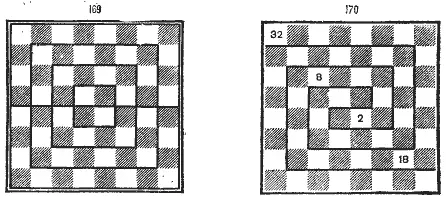
– Нисколько! Число возможных первых ходов фигур и пешек равно числу аминокислот – 20. Если разделить число полей центральных квадратов пополам (рис. 169), то получится ряд: 2-8-18-32. Это равно числу электронов на устойчивых орбитах (в физике!). Махатмы все знали, все! 2, 8, 18, 32 и обратно 32, 18, 8, 2 – строение оболочек элементов (химия!).

– Почему же этого нет в дневнике?

– Потому что автор записи ничего в этом не понимал.

– А что это за сакраментальные цифры 260 и 64?

– 64! Это 4 в кубе! 4 – символизирует аденин (А), гуанин (Г), цитозин (Ц) и тимин (Т). Для 20 аминокислот, требуемых человеку, нужны 64 тройки оснований, так как код их триплетен. Необходимо 4 3= 64. Кстати, 260 = 4 × 65, а 65 – сумма угловых цифр по диагоналям четырех квадратов «насика». 1 + 64, 28 + 37, 40 + 25, 61 + 4! И еще…

– Михаила Николаевича уже невозможно было остановить. Он рисовал в «насике» спираль (рис. 170).

– Это двойная спираль биологического кода, – объяснял он, – с числом полей по большой диагонали – 2, 8, 18, 32! Это как бы 32 группы симметрии в кристаллографии. Кстати, вспомните сетку на «насике», так напоминающую кристаллическую решетку.

Или кристаллические фигуры диагональных квадратов! Но двойная спираль еще и астрономический символ, скажем, схема строения галактик. Но вернемся к учению о жизни. Заметим, что ДНК – это АГЦТ, РНК – АГЦУ. У – урацил – аналог тимина.

Строение ДНК и РНК, то есть дезоксирибонуклеиновая и рибонуклеиновая кислоты, составляющие основу наследственного кода любого существа: и комара, и слона, и человека-по своему строению одинаковы и отражены (пусть символически) в шахматах!

– Сдаюсь! – поднял я руки. – Остановите часы. Впрочем, с часами я не играю. Одно мне ясно, если шахматы хоть в какой-то мере зиждятся на математических или биологических основах, то…