Александр Абрамов - 01-Хождение за три мира (Сборник)

Доминошники снова заняли позицию за столиком под берёзой, но то были другие доминошники, и нашего «типа» среди них не оказалось.

— Чудо окончилось, — сказал я, — пошли подводить итоги.

Мы расселись по креслам в Ганиной комнате, выпили в молчании остывший кофе, закурили вкусные сигареты «Пэл мэл», которые Ганя взял из кабинета отца-композитора, и я рассказал Люде о тёмном трехсекционном тоннеле за аркой ворот.

— Что ты, физик, думаешь о нашем путешествии? — Я намеренно начал с путешествия, оставив истории с машинами на потом.

— Мы опять выскочили из нашего мира.

— Согласен. Куда выскочили?

Он пожал плечами:

— В очередной «мешок».

— Предположим. Но тебе не кажется, что «мешок» на этот раз искусственного происхождения?

— Кажется. Только зачем он нужен?

— Разумный вопрос. Давай-ка ответим на него, а потом подумаем о том, как тоннель связан с пропавшими машинами.

— Думаете, связан?

— Конечно.

Тут Люда подала голос:

— Меня не оставляет ощущение, что «тип в майке» пошутил с вами. Устроил вам прогулку по четвёртому измерению.

— Основания? — Я был строг с оппонентами.

— Очевидная бессмысленность путешествия!

— Тогда цель шутки?

— У шутки может не быть цели, на то она и шутка. Но, если хотите: чтобы вы, наконец, прекратили лезть в чужие дела.

Люда была невежлива, но справедлива. Мы, конечно, мешали кому-то и нам сунули «конфетку»: полакомьтесь, ребятки. Но «конфетка» эта казалась мне вынутой из той же коробки, что и случай с машинами. Логика такова: вы хотите узнать, как это делается? Пожалуйста, погуляйте по тоннелю. Вот так и машины пропадали, понятно?

— Не очень понятно… Как же всё-таки пропадали?

Я поделился сомнениями с ребятами. Люда в ответ только плечами пожала:

— Вас принцип интересует? Да разве в нём дело? Главное — цель опыта. А она-то мне неясна.

— А принцип ясен? — Тут даже Ганя не выдержал.

— Ясен. — Люда оставалась невозмутимой. — Например, треугольник Пенроузов.

Сумасшедший Ганя вскочил с кресла, обнял Люду, чмокнул в щёку, заорал радостно:

— Ну, Людка! Ну, молодец! Это же гениально просто, а я, дурак, не допёр…

Я тоже «не допёр» и тоже почувствовал себя дураком.

— Ладно, гении, сдаюсь. Объясните непосвящённому вашу абракадабру.

Видно, потому, что догадка пришла не к нему, а к Люде, Ганя не стал выламываться, по своему обыкновению, и объяснил:

— Это одна из так называемых «невозможных фигур». Представьте себе модель нашего тоннеля: два перпендикулярных бруска в одной плоскости. Третий брусок перпендикулярен второму и образует с ним другую плоскость, тоже перпендикулярную первой. Если посмотреть на эту фигуру в определённом ракурсе, то наш глаз соединит в одной точке два свободных бруска. Получится треугольник, вернее, проекция на плоскость треугольника, составленного из прямоугольных брусков. — Тут Ганя вооружился карандашом и нарисовал «невозможную фигуру». Вот эту, я сохранил рисунок:

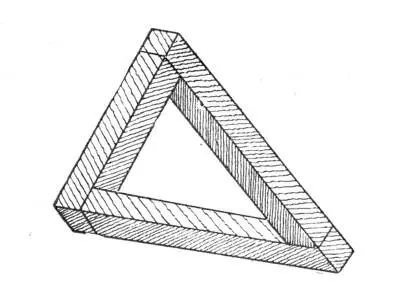
Потом перевернул листок бумаги и начертил мне ещё одну картинку. Вот эту:

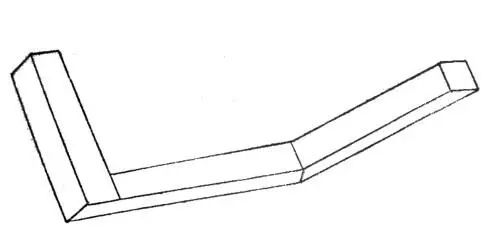
— А вот так она выглядит на самом деле. — Ганя полюбовался на рисунки. — Здорово, а?

— Здорово, — согласился я. — Очень впечатляет. Но какое отношение всё это имеет к нам?

Ганя хотел было ответить, но вмешалась Люда.

— Я считала, что вы соображаете быстрее, — презрительно сказала она, и я молча проглотил явное оскорбление: мне хотелось узнать, что они придумали. — Ваш тоннель — трёхмерная модель четырёхмерной фигуры, с помощью которой машины перемещались в пространстве.

Я, конечно, был глуповат, а она умна, образованна, пытлива, изобретательна и ещё миллион определений из толкового словаря. Я был глуповат и нахален. Я честно признался:

— Ничего не понял. Как мы попали на десятый этаж?

Ганя тяжело вздохнул и сказал Люде:

— Дай я ему объясню. Может, поймёт… Мы прошли по трём коридорам, эквивалентным трём брускам треугольника Пенроузов, и очутились в точке их мнимого касания. Точка эта — квартира с поющей тёткой — находится как раз на одной вертикали с воротами.

— А почему мы не почувствовали подъёма?

Ганя решил быть таким же терпеливым, как Макаренко, Корчак и Сухомлинский, вместе взятые.

— Потому что в четвёртом измерении, где мнимое касание становится действительным, все стороны треугольника лежат в одной горизонтальной плоскости.