Илья Мельников - Рулетка

Так, ещё Н.А.Некрасов, отправляясь на крупную игру, клал деньги, предназначенные для проигрыша, в отдельный карман. "Нужно, – говорил он, – относиться к этим деньгам так, как будто их уже нет". Фортуна любит лёгкость в обращении с деньгами. Если вы станете трястись над каждой ставкой, если вы отрываете деньги от семьи или каких-то своих важных дел, лучше не играйте.

Попробуем проверить, как бы сработала система «Томас Дональд» на практике. Допустим, мы всегда ставим на красное, начальная ставка – $1. Предположим, что из 37 запусков рулетки красное выпадает 18 раз, столько же раз – чёрное, и 1 раз – zero. Пусть красное и чёрное чередуются таким образом: 5 раз красное, 5 раз чёрное, 4 раза красное, 4 раза чёрное, 3 раза красное, 3 раза чёрное, 2 раза красное, 2 раза чёрное, дальше через 1.

Обратите внимание, по результату целой игры мы сыграли вничью, хотя выигрышей у нас было на 1 меньше, чем проигрышей. К тому же, чередование красного и чёрного оказалось для нас очень невыгодным: первые пять раз мы выигрывали всего по $1. Если бы чередование началось с пяти чёрных, то следующие 5 выигрышей принесли бы не $5, а $20 (6+5+4+3+2).

Почему же, даже играя по системе, люди чаще проигрывают в рулетку? Тот же Достоевский, если судить по письмам жене, постоянно просил прислать денег на обратную дорогу. Мы не знаем, по какой системе играл Фёдор Михайлович, но по какой бы ни играл, автор «Игрока» определённо нарушал основные заповеди, касающиеся лёгкого отношения к деньгам. Из его текстов это очевидно.

В наши дни старинная система Томас Дональд подверглась критическому пересмотру со стороны серьёзного математика Льва Натансона. Он рассуждал следующим образом: «Я всегда ставлю на красное. Допустим, начальная ставка – 1 доллар. После выпадения чёрного я увеличиваю ставку на единицу, а после выпадения красного – уменьшаю на единицу. Но что мне делать, если я поставил доллар на красное и выиграл?»

Согласно Т.Дональду, ставка должна оставаться неизменной, так как ни нулевых, ни отрицательных ставок не бывает. «А собственно, почему?» – подумал математик. И попробовал: получилось весьма интересно.

Чтобы не отступать от канонов системы, после ставки на красное и выигрыша, ставку нужно уменьшить на единицу. Если вы ставили $1, следующая ставка должна быть равна нулю. Что такое нулевая ставка, понятно: очередной запуск рулетки вы просто пропускаете. Но при этом вы ставите ноль именно на красное и внимательно следите за тем, что выпадет, – чтобы знать, как поставить в следующий раз. Допустим, опять выпало красное. Вы выиграли и должны снова уменьшить ставку. Следующая ставка (по системе) должна равняться -1 (минус единице).

А что такое отрицательная ставка на красное? Это – ставка на чёрное! Что бы ни случилось в дальнейшем, правило только одно: при выпадении чёрного ставка увеличивается, при выпадении красного – уменьшается.

Пусть, например, при трёх первых запусках рулетки всё время выпадает красное. После первого запуска мы выиграли $1, во второй раз "ставим нуль", а в третий – минус $1 (доллар на чёрное).

Вот пример ещё одной системы, основанной на принципе мартингейл. После каждого выигрыша игрок ставит первоначальную ставку. После каждого проигрыша ставка удваивается и увеличивается на единицу. Игрок всегда ставит на равные шансы.

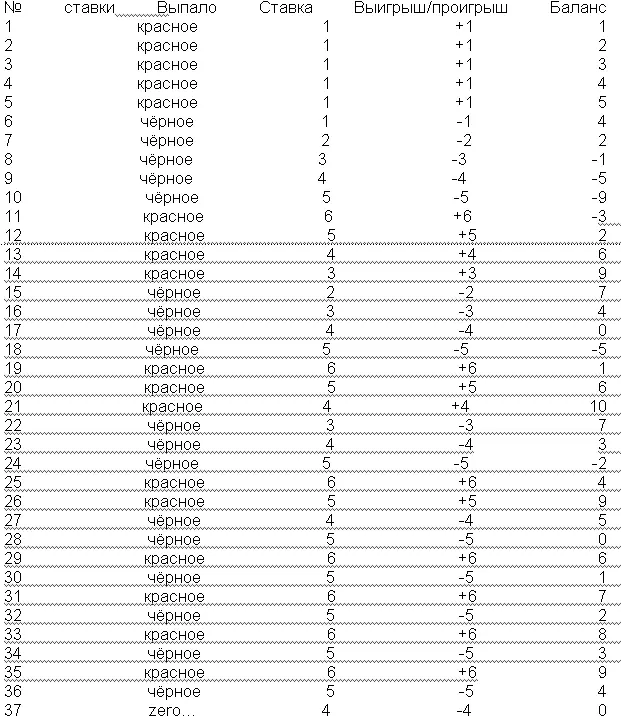
Автор этой системы исходит из предположения, что в игре существуют чередующиеся серии. Отрицательный результат каждой неблагоприятной серии (чёрной полосы) он пытается компенсировать выигрышем в одном-единственном броске.

Нетрудно убедиться, что при каждом положительном исходе его суммарный выигрыш равен порядковому номеру запуска рулетки с начала игры.

Но система столь агрессивна, что применяющий её рискует слишком рано упереться в верхний предел ставки. Посмотрите по таблице, что будет, если в 9-м испытании результат окажется отрицательным.

Следующая ставка должна быть уже в 63 раза больше первоначальной. При нижнем лимите $25 это составит $1575, что намного больше верхнего предела. Серию из 5-ти поражений подряд система уже не выдерживает.