Яков Перельман - Математика в занимательных рассказах

Итак, мы имеем две серии расположений, таких, что положения одной серии могут быть переведены в «нормальное» I, а другой серии — в положение II. И наоборот, мы уже видели, что из «нормального» расположения можно получить любое положение первой серии, а из расположения схемы II — любое положение второй серии. Наконец, два любых расположения, принадлежащие к одной и той же серии, могут быть взаимно переводимы друг в друга: если оба относятся, например, к первой серии, то это значит, что одно из них может быть переведено в положение схемы I, а положение схемы I переводится в другое из данных двух положений; короче — одно данное положение переводимо в другое, и наоборот.

Возникает вопрос: нельзя ли идти дальше и объединить эти два типичных расположения — схем I и II? Это было бы возможно, если бы одно из них переводилось каким-нибудь образом в другое. Тогда обе серии расположений естественно слились бы в одну. Сопоставляя друг с другом расположения схем I и II, можно строго доказать (не станем входить здесь в подробности), что положения эти не могут быть превращены одно в другое никаким числом передвижений. Это — огонь и вода. Поэтому все огромное число размещений шашек распадается на две разобщенные серии: 1) на те, которые могут быть переведены в «нормальное» схемы I: это — положения разрешимые; 2) на те, которые могут быть переведены в положение схемы II и, следовательно, ни при каких обстоятельствах не переводятся в «нормальное» конечное расположение: это — положения неразрешимые, те именно, за разрешение которых тщетно назначались огромные премии.

Но как узнать, принадлежит ли заданное расположение к первой или второй серии? Пример разъяснит это.

Рассмотрим представленное здесь расположение.

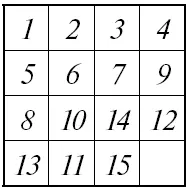
Первый ряд шашек в порядке, как и второй, за исключением последней шашки (9). Эта шашка занимает место, которое в «нормальном» расположении принадлежит 8. Шашка 9 стоит, значит, «ранее» шашки 8; такое упреждение нормального порядка будем называть «инверсией». О шашке 9 мы скажем: здесь имеет место «одна инверсия». Рассматривая дальнейшие шашки, обнаруживаем упреждение для шашки 14; она поставлена на три места (шашек 12, 13, 11) ранее своего нормального положения; здесь у нас 3 инверсии (14 ранее 12; 14 ранее 13; 14 ранее 11). Всего мы насчитали уже 1 + 3 = 4 инверсии. Далее шашка 12 помещена ранее шашки 11, и точно так же шашка 13 — ранее шашки 11. Это дает еще 2 инверсии. Итого имеем, таким образом, 6 инверсий. Подобным образом для каждого заданного расположения устанавливают «общее число инверсий», освободив предварительно последнее место в правом нижнем углу. Если общее число инверсий, как в рассмотренном случае, четное, то заданное расположение может быть приведено к «нормальному» конечному; другими словами, оно принадлежит к разрешимым. Если же число инверсий нечетное, то данное расположение принадлежит ко второй серии, т. е. к неразрешимым.

За недостатком места мы должны отказаться от строгого доказательства всего изложенного. Но можно наметить кратко главные этапы в ходе этого доказательства. Среди ходов будем различать «горизонтальные» и «вертикальные» (смысл этих слов, конечно, ясен). Легко видеть, что всякий «вертикальный» ход изменяет число инверсий либо на 1, либо на 3, т. е. на нечетное число. Чтобы одно положение шашек перевести в какое-либо другое, необходимо сделать h горизонтальных и v вертикальных ходов, причем — если в обоих положениях свободное поле находится в правом нижнем углу — оба числа, h и v, четные. Горизонтальные ходы не могут изменить инверсий, вертикальные же изменяют их каждый раз на нечетное число, т. е. в общем итоге — так как v число четное — на четное число. Вот почему для переводимости двух расположений (в которых пустое поле находится в правом нижнем углу) одного в другое необходимо, чтобы они различались между собою четным числом инверсий. Это условие взаимного перевода является притом не только необходимым, но, очевидно, также и достаточным. — «Нормальное» расположение имеет 0 инверсий, и, следовательно, ему соответствует серия положений с четным числом инверсий (при условии, что свободное поле на одном и том же месте). Расположение II имеет одну инверсию, — его серия есть серия нечетных инверсий.

Поучительной в этой игре является и ее история. При своем появлении игра вызвала всюду, как мы уже рассказывали, сильнейшее, прямо лихорадочное возбуждение и породила настоящую манию игры. С этой лихорадкой удалось справиться только математике. И удалось ей это так полно, что в наши дни подобная страстность в этой игре уже совершенно немыслима. Победа достигнута была благодаря тому, что математика создала исчерпывающую теорию игры, теорию, не оставляющую в ней ни одного сомнительного пункта и превратившую ее в образчик настоящей математической игры. Исход игры зависит здесь не от каких-либо случайностей и даже не от исключительной находчивости, как в других играх, а от чисто математических факторов, предопределяющих исход с безусловной достоверностью. [37] «Такен (игра в 15), — говорит французский математик Люка, — не только весьма интересная игрушка, но также и прибор, с помощью которого чрезвычайно легко дать наглядное понятие об одном из важнейших отделов алгебры, а именно о теории определителей, принадлежащей Лейбницу. Поэтому теорию и практические приемы игры в такен можно считать своего рода подготовкой к изучению этой части алгебры». — Ред.