Яков Перельман - Фокусы и игры

Рис. 10. Что кривее?

Какая из трех бумажных полосок, изображенных на рис. 11, самая длинная?

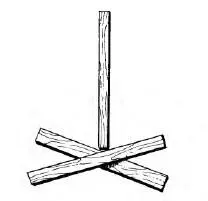
Рис. 11. Что длиннее?

Перед вами (рис. 12) два корабля: пароход и парусник. У кого из них палуба длиннее?

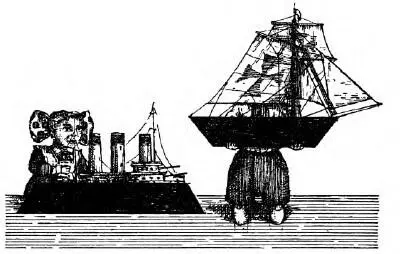
Рис. 12. Равны ли палубы?

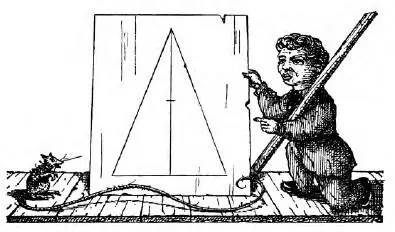
Рис. 13. Где середина?

Школьника спросили, где находится середина высоты начерченного здесь треугольника (рис. 13). Он указал место, обозначенное на фигуре черточкой. Поправьте мальчика, определив середину на глаз, а затем проверьте его и себя, линейкой.

Школьник начертил два прямоугольника пересеченных прямой линией, и утверждал, что эти прямоугольники равны (рис. 14). Почему он думал, что они равны?

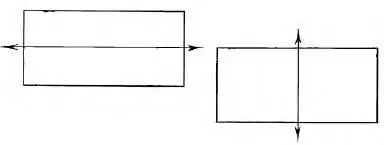
Рис. 14. Одинаковы ли эти прямоугольники?

Я показывал своим знакомым картинку, представленную здесь на рис. 15, и они утверждали, что прямоугольник, описанный около шляпы иностранца, имеет форму квадрата. В чем их ошибка?

Рис. 15. Квадрат ли здесь?

Если продолжить прямую линию ab (рис. 16), то куда она упрется: выше точки с или ниже?

Какая из линий ab, cd и ef (рис. 17) самая длинная?

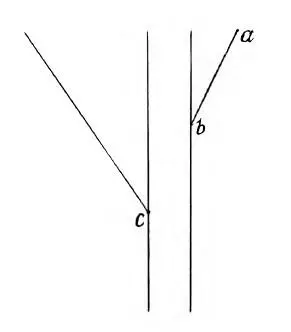
Рис. 16. Куда упрется линия?

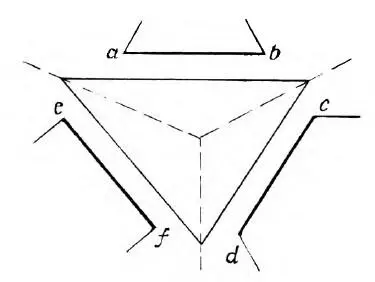
Рис. 17. Сравните ab, cd и ef

Поместится ли в промежутке между AB и CD (рис. 18) изображенный здесь кружок?

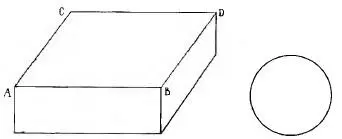
Рис. 18. Поместится ли кружок между AB и CD?

На рис. 19 вы видите два заштрихованных кружка, которые кажутся одинаковых размеров. Однако вы натренировали свой глазомер предыдущими упражнениями и, конечно, не попадете впросак.

Вам нетрудно будет ответить на вопрос: какой кружок больше?

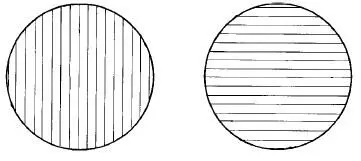
Рис. 19. Какой кружок больше?

1. Зрачки на рисунке кажутся движущимися по той же причине, по которой оживают картины кинематографа. Когда мы смотрим на правый рисунок и затем быстро переводим взгляд на левый, то первое зрительное впечатление исчезает не сразу, а еще сохраняется на мгновение; в тот момент, когда оно исчезнет и заменится новым, нам, естественно, должно показаться, что зрачки на рисунке передвинулись от одного края глаза к другому.

2. Ваше решение, вероятно, было приблизительно таким (рис. 20).

Рис. 20. Кажущееся (неправильное) решение задачи с тремя монетами

Оно как будто вполне верно удовлетворяет условию задачи, не правда ли? Но попробуйте измерить расстояние циркулем – окажется, что вы ошиблись чуть ли не в полтора раза!

А вот правильное расположение монет, хотя на глаз оно кажется совсем неправильным (рис. 21).

Чем крупнее кружки, тем обман зрения поразительнее. Опыт хорошо удается и в том случае, если взять неодинаковые кружки.

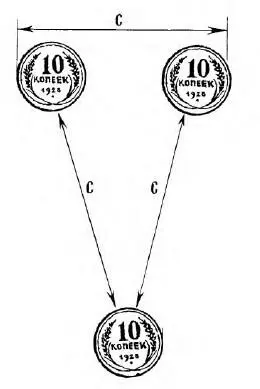
Рис. 21. Правильное решение задачи с тремя монетами

3. Все четыре фигуры одинаковой величины, хотя нам и кажется, что они уменьшаются слева направо. В каждой паре правая фигура представляется меньше оттого, что левая расширяется по направлению к правой и словно охватывает ее.