Яков Перельман - Головоломки. Выпуск 2

Итак, встреча стрелок случится спустя 5 1/ 11мин после часа дня, т. е. в 5 1/ 11мин второго.

Когда же произойдет следующая встреча?

Нетрудно сообразить, что это случится через 1 час 5 1/ 11мин, т. е. в 2 ч 10 1/ 2мин. Следующая – спустя еще 1 час 5 5/ 11мин, т. е. в 3 ч 16 4/ 11мин, и т. д. Всех встреч, как легко видеть, будет 11; последняя наступит через 1 1/ 11× 11 = 12 ч после первой, т. е. в 12 ч; другими словами, очередная встреча стрелок совпадает с самой первой и дальнейшие встречи повторятся снова в известные моменты.

Вот полный перечень встреч:

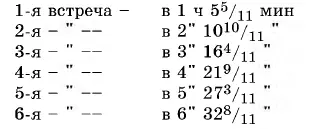
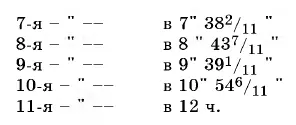
2. Эта задача решается весьма сходно с предыдущей. Начнем опять с 12 ч, когда положение стрелок одинаково. Нужно вычислить, сколько времени потребуется для того, чтобы минутная стрелка обогнала часовую ровно на полкруга – тогда стрелки и будут направлены как раз в противоположные стороны. Мы уже знаем (см. предыдущую задачу), что в течение целого часа минутная стрелка обгоняет часовую на 1/ 11 полного круга; чтобы обогнать ее всего на 1/ 2круга, понадобится меньше времени, чем целый час. Причем, во столько раз, во сколько 1/ 2меньше 1/ 12, т. е. потребуется всего 6/ 11ч. Значит, после 12 часов стрелки в первый раз располагаются одна против другой спустя 6/ 11ч, или 32 8/ 11мин. Взгляните на часы, когда стрелки направлены в противоположные стороны.

Единственный ли это момент, когда стрелки так расположены? Конечно, нет. Такое положение стрелки занимают спустя 32 8/ 11минуты после каждой встречи. А мы уже знаем, что встреч бывает 11 в течение двенадцати часов; значит, и располагаются стрелки врозь тоже 11 раз в течение 12 часов. Найти эти моменты нетрудно:

12 ч + 32 8/ 11мин = 12 ч 32 8/ 11мин,

1 ч 5 5/ 11мин + 32 8/ 11мин = 1 ч 38 7/ 11мин,

2 ч 10 10/ 11мин + 32 8/ 11мин = 2 ч 43 7/ 11мин,

3 ч 16 1/ 11мин + 32 8/ 11мин = 3 ч 49 1/ 11 мин и т. д.

Вычислить остальные моменты предоставляю вам самим.

3. Если начать наблюдение за стрелками ровно в 12 часов, то в течение первого часа мы искомого расположения не заметим. Почему? Потому что часовая стрелка проходит 1/ 12того, что проходит минутная, и, следовательно, отстает от нее гораздо больше, чем требуется. На какой бы угол ни отошла от 12 минутная стрелка, часовая повернется на 1/ 12этого угла, а не на 1/ 2, как нам требуется. Но вот прошел час; теперь минутная стрелка стоит у 12, часовая – у 1, на 1/ 12полного оборота впереди минутной. Посмотрим, не может ли такое расположение стрелок наступить в течение второго часа. Допустим, что момент этот наступил тогда, когда часовая стрелка отошла от цифры 12 на долю полного оборота, которую мы обозначим через х. Минутная стрелка успела к этому времени пройти в 12 раз больше, т. е. 12 × х. Если вычесть отсюда один полный оборот, то остаток 12 × х – 1 должен быть вдвое больше, чем х, т. е. равняться 2 × х.

Итак, 12 × х – 1 = 2 × х, откуда следует, что 1 целый оборот равен 10 × х (действительно, 12 × х-10 × х = 2 × х). Но если 10 × х = = целому обороту, то х = 1/ 10части оборота. Вот и решение задачи: часовая стрелка отошла от цифры 12 на 1/ 10полного оборота, на что требуется 12/ 10ч, или 1 ч 12 мин. Минутная стрелка при этом будет вдвое дальше от 12, т. е. на расстоянии 1/ 5оборота; это соответствует 60/5 = 12 мин – как и должно быть.

Мы нашли одно решение задачи. Но есть и другие: стрелки в течение двенадцати часов располагаются таким же образом не один раз, а несколько. Попытаемся найти остальные решения.

Для этого дождемся двух часов; минутная стрелка стоит у 12, а часовая – у 2. Рассуждая, как прежде, получаем равенство

12 × х – 2 = 2 × х ,

откуда 2 целых оборота равны 10 × х и, значит, х = 1/ 5целого оборота. Часы будут показывать при этом 12/ 5= 2 ч 24 мин.

Дальнейшие моменты читатель легко вычислит сам и найдет, что стрелки располагаются согласно требованию задачи в следующие 10 моментов:

в 1 ч 12 мин

в 2 ч 24 мин

в 3 ч 36 мин

в 4 ч 48 мин

в 6 ч

в 7 ч 12 мин

в 8 ч 24 мин

в 9 ч 36 мин

в 10 ч 48 мин

в 12 ч.

Ответы: «в 6 часов» и «в 12 часов» могут показаться неверными, – но только с первого взгляда. Действительно, в 6 часов часовая стрелка стоит у 6, минутная – у 12, т. е. ровно вдвое дальше от начальной отметки 12 (успев описать один оборот). В 12 же часов часовая стрелка удалена от 12 на нуль, а минутная, если хотите, на «два нуля» (потому что двойной нуль – то же, что и нуль); значит, и этот случай, в сущности, удовлетворяет условию задачи.