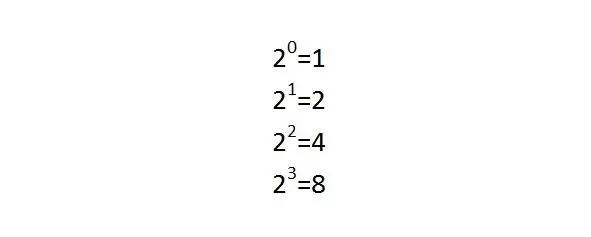Станислав Баранов - Фридрих - VLS (RLS) за полгода. Часть 3. Winter Variation, No Edges, Summer Variation, Edge Control

Но самое интересное, что каждую группу можно условно разбить на 8 условных подгрупп. Не знаю, делал ли так, кто-то из изучающих и придумавших метод, но в своих книгах я так сделал. Как же так 8 групп, а алгоритмов 27. Ведь 27 не делится на 8. Но каждая подгруппа содержит количество алгоритмов, определяемых степенью 2n, где n=0, 1, 2, 3: 1, 2, 4 или 8 алгоритмов.

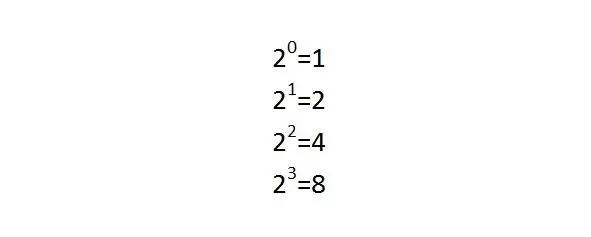
Число алгоритмов в группе VLS

Самое маленькое и самое большое число алгоритмов (1 или 8) содержат первая и последняя подгруппа. А 2 или 4 алгоритма содержат по три подгруппы (средние).

Тогда общее число алгоритмов в группе получается 27=1*1+3*2+3*4+1*8 (1 подгруппа с 1 алгоритмом, 3 подгруппы по 2 алгоритма, 3 подгруппы по 4 алгоритма, 1 подгруппа с 8 алгоритмами).

Название первой подгруппы в каждой группе я называю определяющим, и дающим название группы: группа Стелса, группа Человека, группа Снежинки, группа Полного, группа Коряги и т. п.

Данная группа это группа Полного (Жерар Депардье). С помощью запоминалки, я могу вспомнить всю группу. Далее по названию подгруппы и определяющему числу могу вспомнить конкретную историю (запоминалку), а уже по ней вспомнить формулу решения.

Не нужно переживать, что много историй останется в голове. Через некоторое время запоминалки исчезнут – останется картинка случая и навык вращения (так у меня произошло при изучении метода Фридрих).

Получается примерно такая структура.

Структура группы Полного

Далее я заполняю некоторыми данными, и в таком виде как картинка она тоже есть в моей голове.

Рисунок

Полный 400 (WVLS01)

Случай назван Полный 400 (WVLS01).

Решение VLS Полный 400 (WVLS01)

1_ 8) U L 1U2 R U R 1U2 L = U L 1 – U2 (R U R 1 U 1) – U 1 L = U – L 1 U2 (R U R 1) – U2 L = U + (L 1 U2 R) U (R 1 U2 L)

2_ 8) U 1L 1U2 R U 1R 1U2 L = U 1 L 1 U – (U R U 1 R 1) U2 L = U 1 – L 1 U2 (R U 1 R 1) U2 L =U 1 + (L 1 U2 R) U 1 (R 1 U2 L)

3_ 8) y 1U – Rw D – (Rw 1U 1Rw) – D 1Rw 1 = Dw – Rw D – (Rw 1 U 1 Rw) – D 1 Rw 1 = Dw (Rw D Rw 1) – U 1 (Rw D 1 Rw 1)

4_ 11) (R2 D R 1) U (R D 1R2) – (U R U 1 R 1)

5_ 7) Lw 1 (U2 R U2 Rw 1) U2 L = (Lw 1 U2 R) U2 (Rw 1 U2 L)

6_ 12) U R U 1 – (R D R 1) U R D 1R 1U 1 R 1= (U R U 1 R 1) – (R2 D R 1) U (R D 1 R2) – (R U 1 R 1)

7_ 8) y U (Lw D Lw 1) – U 1(Lw D 1 Lw 1)

Как запомнить?

1) Вообще 1-я и 2-я формулы одинаковые, но в одной вращение верха идёт по часовой стрелки, а в другой против часовой. Стороны L R сначала поднимаются, потом опускаются в обратном порядке. Один алгоритм крутится с одной позиции пары спереди, а другой с позиции пары сзади.

Можно принять, что по часовой стрелке это пара ушла вперед. А против часовой стрелки это пара ушла назад. Таким образом, лего запоминается, что пару нужно всегда вращать в ту сторону, куда ушла от первоначального положения. Получается формулы 1-я, 2-я и 5-я образуют для этого случая своеобразный expert-VLS.

Ходы (U L 1) запоминаем образом улыбки.

Ходы U 1 L запоминаем образом девушки по имени Юля (у каждого своя знакомая девушка с таким именем).

Запоминалка: «Полный 400кг-й улыбающийся Вова хот-дог Юле отдал».

2) Смотри пункт 1).

3)

4) Пиф-пафы (R2 D R 1) и (R D 1 R2) названы дед и бабушка.

Пиф-паф (R2 D R 1) U (R D 1 R2) назван репка.

Запоминалка: «Полный 400кг-ю репку скинул в западню».

5) Данный алгоритм я нашёл на сайте http://www.cyotheking.com. Далее проверка показала, что никаких больше неповторяющихся с сайтом algdb.net алгоритмов не оказалось.

Алгоритм простой и мне не понадобилась запоминалка. Так как он имеет цикл (сам себя моделирует и решает), то его можно крутить сколь угодно долго – пока не будет получаться очень быстро.

Этот алгоритм напоминает аналогичные 1-й и 2-й.

6) Пиф-паф (R2 D R 1) U (R D 1 R2) назван репка.

Запоминалка: «Полный 400кг-й попал в западню к репке, и включил заднюю передачу».

Пиф-паф (R2 D R 1) U (R D 1 R2) назовём репка в силу ассоциации с буквы U c русской письменной буквой u , и словами дед и бабка.

Запоминалка: «Полный выкопал 400кг репки из западни выкопал 400кг репки». Далее понятная трехходовка.

7) Данный алгоритм из видео Easiest Winter Variation (OLL Skip) Cases( https://www.youtube.com/watch?v=rbRJWAH_pts)

Как смоделировать случай?

Lw 1 (U2 R U2 Rw 1) U2 L (сам себя моделирует)

(R U R 1U 1) – (R2 D R 1) U 1(R D 1 R2)