Михаил Горбачев - Новейший самоучитель безопасного вождения

Первым предложил использовать окружность для графического изображения работы шины в повороте профессор Вунибальд Камм (1893–1966), работавший в техническом университете в городе Штутгарт, в Германии. Вероятно, прежде чем господин Камм пришел к выводу, что можно графически изобразить запас сцепления шины в повороте, он так же покружил с тарелкой супа в руках. Только это был не борщ, а немецкий айнтопф, но на результаты эксперимента это не повлияло.

Итак, силы, действующие на шину в повороте, можно изобразить векторами. Эта сила может быть большой, средней или нулевой. Измерять ее нет никакой необходимости, для нашего графика это неважно (рис. 13). Важно только что длина стрелки изображает – максимум, половина стрелки – середину максимума и ноль – ничего. Направление стрелки возможно в любую сторону, поэтому обведем вокруг окружность. Расстояние от центра до окружности изображает в данном случае максимальное боковое или продольное ускорение. Что происходит на линии окружности? Это и есть зона турбулентности, здесь силы сцепления иссякают и уступают место силам скольжения. В этой зоне достигается максимальное сцепление шины с дорожным покрытием, шины находятся в состоянии контролируемой нестабильности. Окружность профессора Камма наглядно показывает, что тормозить и разгоняться в повороте можно, важно только правильно распределить соотношение сил продольных и поперечных ускорений. Конечно, на практике все намного сложнее, но это помогает понять принцип работы шины в повороте. Скажу по секрету, что благодаря этой теории и была изобретена антиблокировочная система тормозов.

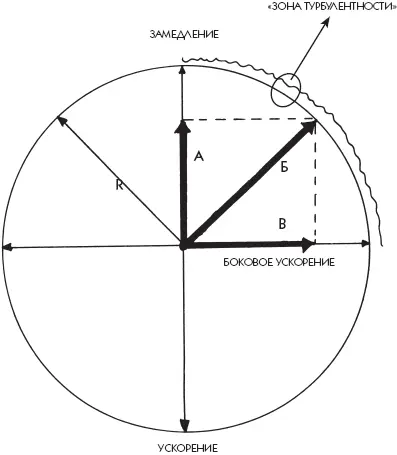
Рис. 13

График показывает, что в данном повороте при боковых ускорениях «В», мы можем тормозить настолько интенсивно «Б», чтобы результирующий вектор «Б» был не больше, чем окружность, определяющая предел сцепления шин.

На границе окружности шина теряет сцепление и автомобиль становится неуправляемым.

Поверхность полусферы профессора Камма (рис. 14) показывает вертикальное ускорение. Мы говорили о том, что вершина поворота может находиться на холме или на изломе. В этот момент машина станет легче, а вектор устремится в направлении поверхности полусферы, снижая сцепление шины с покрытием дороги. В этот момент способность шины поворачивать, разгоняться или тормозить сильно ограничена. За разгрузкой подвески последует ее сжатие, и неизбежно возникнет прижимная сила – вес машины увеличится, сцепление шин улучшится. Графически это показывается увеличением окружности, отодвигающей зону начала скольжения. Это самый подходящий момент, чтобы тормозить или поворачивать.

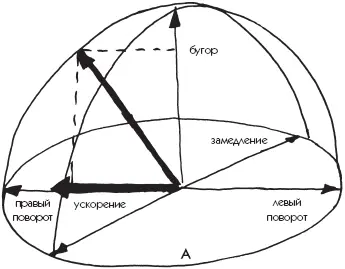
Рис. 14

При проезде бугра автомобиль становится легче, и его возможности тормозить и поворачивать снижаются.

При проезде впадины – наоборот, окружность полусферы становится больше, значит, сцепление шин увеличивается под воздействием дополнительной нагрузки.

Подведем итог и суммируем вышесказанное. Управление автомобилем в движении создает силы, действующие на машину. Водитель может эти силы в процессе «борьбы» с дорогой и машиной увеличивать или уменьшать, но они все равно будут подчиняться законам физики. Грамотное управление автомобилем состоит в умении водителя понимать и не нарушать эти законы, а умело их использовать. Быстро, но безопасно ехать на автомобиле – значит умело балансировать на границе окружности профессора Камма (рис. 15) . А в балансе главное чувствовать перемещение веса и не перебарщивать с ним. Иначе ваш борщ выплеснется из тарелки!

Рис. 15

Быстро, но безопасно ехать на автомобиле – значит умело балансировать на границе окружности. А в балансе главное чувствовать перемещение веса.

Итак, давайте разберемся, в чем состоит принцип работы вспомогательных систем. Начнем с ESP (Electronic Stability Programm) – электронной системы курсовой стабилизации. Можно ли при наличии такой системы, особо не задумываясь, вваливать в повороты, – задаст вопрос водитель, предпочитающий агрессивный стиль вождения? Сработает ли она как страховка у альпиниста, или как сетка в цирке, натянутая под воздушными гимнастами?