Джесси Шелл - Геймдизайн [Как сознание определяет наше бытие] [litres]

Шанс, что двойная шестерка выпадет после одного броска, равен 1/36. Итак, согласно правилу 7, вероятность того, что двойная шестерка не выпадет, – 1 – 1/36, или 35/36.

То есть, если применить правило 6 (умножение), шанс на то, что двойная шестерка не выпадет ни разу при 24 бросках, составит 35/36 × 35/36 двадцать четыре раза, или, чтобы было понятнее, 35/36 в 24-й степени. Вы вряд ли захотите делать все эти подсчеты вручную, но если взять калькулятор, то вы увидите, что ответ – 0,5086, или 50,86 %. Но это вероятность проигрыша шевалье. Чтобы вычислить вероятность его выигрыша, нам нужно применить правило 7 еще раз: 1 – 0,5086 = 49,14 %. Теперь понятно, почему он проигрывал. Шанс на победу был настолько близким к половине, что его трудно было отличить от шанса на поражение, но после большого количества игровых сессий стало понятно, что поражение было более вероятным исходом.

Несмотря на то что все вопросы, связанные с вероятностью, можно решить посредством перечисления, правило 7 поможет вам сохранить много времени. На самом деле, это же правило мы могли бы применить и для первой игры шевалье.

Правило 8: Сумма нескольких линейных случайных исходов – это НЕ линейный случайный исход!

Не паникуйте. Как бы сложно это ни звучало, на самом деле все просто. «Линейный случайный исход» – это просто случайное событие, в котором все результаты имеют одинаковую вероятность. Бросание игральной кости – это отличный пример линейного случайного выбора. Хотя, если бросить несколько игральных костей, то возможные результаты НЕ будут иметь одинаковую вероятность. Если вы, например, бросаете две кости, то шанс получить семь довольно высок, в то время как шанс получить 12 намного меньше. Перечислив все возможности, вы поймете, почему так получается:

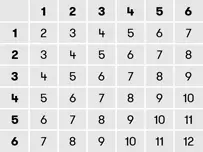
Посмотрите, как много в этой таблице 7 и всего одно 12! Мы можем продемонстрировать это на диаграмме под названием «Кривая распределения вероятности», чтобы увидеть шансы каждого из результатов.

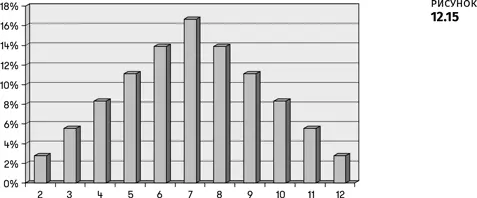
Правило 8 кажется довольно очевидным, но я часто вижу, как начинающие дизайнеры составляют вместе два случайно выбранных числа, не понимая эффекта этого сложения. А иногда это именно тот эффект, который вам нужен, например, в игре Dungeons and Dragons игрок зарабатывает (виртуальные) очки навыков достоинством от 3 до 18, бросая три обычные (шестигранные) игральные кости. В результате в игре доминируют навыки достоинством 10 или 11, а 3 или 18 встречаются крайне редко, и это именно то, чего хотел дизайнер. А теперь представьте, насколько сильно игра отличалась бы от оригинальной версии, если бы, зарабатывая очки, игроки бросали один двадцатигранный кубик?

Геймдизайнеры, собирающиеся использовать механику шанса как инструмент для создания своих игр, должны понимать, какая кривая распределения вероятности нужна именно им, а также знать, как ее получить. С опытом к вам придет понимание того, насколько ценными инструментами могут быть кривые распределения вероятности.

Правило 9: Бросайте кости

Все вероятности, о которых мы говорили до этого, были теоретическими вероятностями, иными словами, тем, что должно случиться. Существует также практическая вероятность, которая является мерой того, что уже случилось. Например, если бросить кость, теоретическая вероятность выпадения шестерки составит ровно 1/6, или около 16,67 %. Но я мог бы вычислить практическую вероятность, бросив игральную кость 100 раз и записав, сколько раз мне попадались шестерки. Мне могут выпасть 20 шестерок из 100. В этом случае практическая вероятность составит 20 %, что не слишком сильно отличается от теоретической вероятности. Конечно, с увеличением количества попыток практическая вероятность все больше приближается к теоретической. Это правило получило название «метод Монте-Карло» в честь знаменитого казино.

Положительной чертой использования метода Монте-Карло для вероятности является то, что он не требует сложных математических подсчетов – вы проделываете одно и то же действие много раз и просто записываете результаты. Иногда результаты подобных тестов могут быть полезнее теоретической вероятности потому, что здесь мы имеем дело с реальными сущностями. Если существуют факторы, которые нельзя учесть при математических подсчетах (возможно, центр тяжести вашего кубика немного смещен к шестерке), или же эти подсчеты настолько сложные, что вы не можете составить теоретическую картину вашей ситуации, метод Монте-Карло – это то, что вам нужно. Шевалье мог бы легко ответить на свой вопрос, бросая кости снова и снова, считая количество побед и разделяя их на число сделанных попыток.