Douglas Hofstadter - I Am a Strange Loop

The lower line in our display starts out with 3, so our conjecture would imply that all the other numbers in that line are gotten by adding various multiples of 4 to 3, and consequently, that every number in that line is of the form 4 n + 3. Likewise (if we ignore the initial misfit of 2), the first number in the upper line is 5, so if our conjecture is true, then every subsequent number in that line is of the form 4 n + 1.

Well, well — our conjecture has suggested a remarkably simple pattern to us: Primes of the form 4 n + 1 can be represented as sums of two squares, while primes of the form 4 n + 3 cannot. If this guess is correct, it establishes a beautiful, spectacular link between primes and squares (two classes of numbers that a priori would seem to have nothing to do with each other), one that catches us completely off guard. This is a glimpse of pure magic — the kind of magic that mathematicians live for.

And yet for a mathematician, this flash of joy is only the beginning of the story. It is like a murder mystery: we have found out someone is dead, but whodunnit? There always has to be an explanation. It may not be easy to find or easy to understand, but it has to exist.

Here, we know (or at least we strongly suspect) that there is a beautiful infinite pattern, but for what reason ? The bedrock assumption is that there is a reason here — that our pattern, far from being an “infinite coincidence”, comes from one single compelling, underlying reason; that behind all these infinitely many “independent” facts lies just one phenomenon.

As it happens, there is actually much more to the pattern we have glimpsed. Not only are primes of the form 4 n + 3 never the sum of two squares (proving this is easy), but also it turns out that every prime number of the form 4 n + 1 has one and only one way of being the sum of two squares. Take 101, for example. Not only does 101 equal 100 + 1, but there is no other sum of two squares that yields 101. Finally, it turns out that in the limit, as one goes further and further out, the ratio of the number of Class A primes to the number of Class B primes grows ever closer to 1. This means that the delicate balance that we observed in the primes below 100 and conjectured would continue ad infinitum is rigorously provable.

Although I will not go further into this particular case study, I will state that many textbooks of number theory prove this theorem (it is far from trivial), thus supplementing a pattern with a proof. As I said earlier, X is true because X has a proof, and conversely, X is true and so X has a proof.

The Long Search for Proofs, and for their Nature

I mentioned above that the question “Which numbers are sums of two primes?”, posed almost 300 years ago, has never been fully solved. Mathematicians are dogged searchers, however, and their search for a proof may go on for centuries, even millennia. They are not discouraged by eons of failure to find a proof of a mathematical pattern that, from numerical trends, seems likely to go on and on forever. Indeed, extensive empirical confirmation of a mathematical conjecture, which would satisfy most people, only makes mathematicians more ardent and more frustrated. They want a proof as good as Euclid’s, not just lots of spot checks! And they are driven by their belief that a proof has to exist — in other words, that if no proof existed, then the pattern in question would have to be false.

This, then, constitutes the flip side of the Mathematician’s Credo:

X is false because there is no proof of X;

X is false and so there is no proof of X.

In a word, just as provability and truth are the same thing for a mathematician, so are nonprovability and falsity. They are synonymous.

During the centuries following the Renaissance, mathematics branched out into many subdisciplines, and proofs of many sorts were found in all the different branches. Once in a while, however, results that were clearly absurd seemed to have been rigorously proven, yet no one could pinpoint where things had gone awry. As stranger and stranger results turned up, the uncertainty about the nature of proofs became increasingly disquieting, until finally, in the middle of the nineteenth century, a powerful movement arose whose goal was to specify just what reasoning really was, and to bond it forever with mathematics, fusing the two into one.

Many philosophers and mathematicians contributed to this noble goal, and around the turn of the twentieth century it appeared that the goal was coming into sight. Mathematical reasoning seemed to have been precisely characterized as the repeated use of certain basic rules of logic, dubbed rules of inference, such as modus ponens : If you have proven a result X and you have also proven X ⇒ Y (where the arrow represents the concept of implication, so that the line means “If X is true, then Y is also true”), then you can toss Y into the bin of proven results. There were a few other fundamental rules of inference, but it was agreed that not very many were needed. About a decade into the twentieth century, Bertrand Russell and Alfred North Whitehead codified these rules in a uniform if rather prickly notation (see facing page), thus apparently allowing all the different branches of mathematics to be folded in with logic, making a seamless, perfect unity.

Thanks to Russell and Whitehead’s grand work, Principia Mathematica, people no longer needed to fear falling into hidden crevasses of false reasoning. Theorems were now understood as simply being the bottom lines of sequences of symbol-manipulations whose top lines were either axioms or earlier theorems. Mathematical truth was all coming together so elegantly. And as this Holy Grail was emerging into clear view, a young boy was growing up in the town of Brünn, Austro-Hungary.

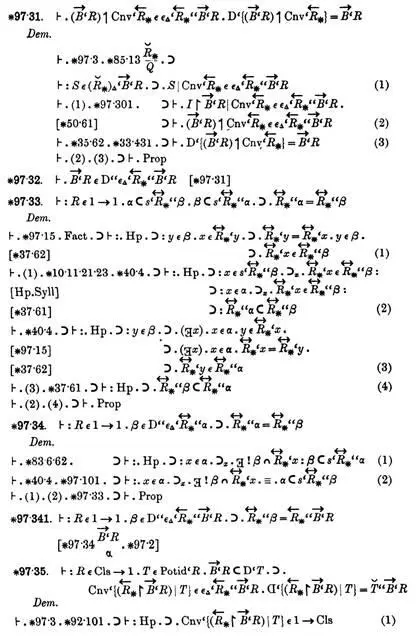
CHAPTER 10

Gödel’s Quintessential Strange Loop

Gödel Encounters Fibonacci

BY HIS early twenties, the boy from Brünn was already a superb mathematician and, like all mathematicians, he knew whole numbers come in limitless varieties. Aside from squares, cubes, primes, powers of ten, sums of two squares, and all the other usual suspects, he was familiar with many other types of integers. Most crucially for his future, young Kurt knew, thanks to Leonardo di Pisa (more often known as “Fibonacci”), that one could define classes of integers recursively.

In the 1300’s, Fibonacci had concocted and explored what are now known as the “Fibonacci numbers”:

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, . . .

In this rapidly growing infinite sequence, whose members I will henceforth refer to as the F numbers, each new element is created by summing the two previous ones (except for the first pair, 1 and 2, which we simply declare by fiat to be F numbers).

This almost-but-not-quite-circular fashion of defining a sequence of numbers in terms of itself is called a “recursive definition”. This means there is some kind of precise calculational rule for making new elements out of previous ones. The rule might involve adding, multiplying, dividing, whatever — as long as it’s well-defined. The opening gambit of a recursive sequence (in this case, the numbers 1 and 2) can be thought of as a packet of seeds from which a gigantic plant — all of its branches and leaves, infinite in number — grows in a predetermined manner, based on the fixed rule.