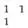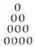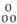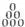Михаил Филиппов - Блез Паскаль. Его жизнь, научная и философская деятельность

Приводим вкратце решение Паскаля. Предположим, говорит Паскаль, что играют два игрока и что выигрыш считается окончательным после победы одного из них в трех партиях. Предположим, что ставка каждого игрока составляет 32 червонца и что первый уже выиграл две партии (ему не хватает одной), а второй выиграл одну (ему не хватает двух). Им предстоит сыграть еще партию. Если ее выиграет первый, он получит всю сумму, то есть 64 червонца; если второй, у каждого будет по две победы, шансы обоих станут равны, и в случае прекращения игры каждому, очевидно, надо дать поровну.

Итак, если выиграет первый, он получит 64 червонца. Если выиграет второй, то первый получит лишь 32. Поэтому, если оба согласны не играть предстоящей партии, то первый вправе сказать: 32 червонца я получу во всяком случае, даже если я проиграю предстоящую партию, которую мы согласились признать последней. Стало быть, 32 червонца мои. Что касается остальных 32 – может быть, их выиграю я, может быть, и вы; поэтому разделим эту сомнительную сумму пополам. Итак, если игроки разойдутся, не сыграв последней партии, то первому надо дать 48 червонцев, или же 3/4 всей суммы, второму 16 червонцев, или у, из чего видно, что шансы первого из них на выигрыш втрое больше, чем второго (а не вдвое, как можно было бы подумать при поверхностном рассуждении).

Нетрудно видеть, что теория вероятностей имеет огромное применение. Посредством нее астрономы определяют вероятные ошибки наблюдений, артиллеристы вычисляют вероятное количество снарядов, могущих упасть в определенном районе, физики оценивают число частиц газа, ударяющих о стенки сосуда, страховые общества – размер премий и процентов, уплачиваемых при страховании жизни и имущества. Во всех случаях, когда явления чересчур сложны, чтобы допустить абсолютно достоверное предсказание, теория вероятностей дает возможность получить результаты, весьма близкие к реальным и вполне годные на практике.

Работы над теорией вероятностей привели Паскаля к замечательному математическому открытию, еще и теперь не вполне оцененному. Он составил так называемый арифметический треугольник, позволяющий заменять многие весьма сложные алгебраические вычисления простейшими арифметическими действиями.

Чтобы получить треугольник Паскаля, напишем горизонтальный ряд, составленный из единицы, повторенной сколько угодно раз: 1, 1, 1, 1 и т. д., и такой же вертикальный ряд. Дальнейшие числа треугольника получаются так: любое число треугольника Паскаля равно сумме числа стоящего над ним, с числом, стоящим слева от него. Так, например, написав сначала

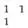
вставляем затем число 2 таким образом:

потому что 2=1+1. Продолжая подобные действия, нетрудно составить, например, следующий треугольник Паскаля:

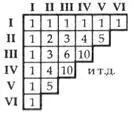
Первая строка (и первый столбец) состоит из единицы, повторенной несколько раз; вторая строка (и столбец) – из натуральных чисел 1, 2, 3, 4, 5 и т. д.; третья строка (и столбец) – из так называемых треугольных чисел 1, 3, 6, 10 и т. д.; в четвертой строке (и столбце) стоят пирамидальные числа 1, 4, 10 и т. д.

Чтобы понять смысл этих названий, предположим, что требуется узнать сразу, сколько ядер находится в куче, имеющей вид треугольника, например, такой:

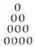
Сначала положено 1 ядро, потом 2, 3, 4 и т. д. Словом, имеем ряд натуральных чисел. Легко убедиться, что искомая сумма равна тому числу в треугольнике Паскаля, которое стоит непосредственно под последним из слагаемых натуральных чисел. Так, в нашем примере под числом 4 стоит 10, и действительно 1+2+3+4=10. Число 10 обозначает число ядер в треугольной кучке, стороны которой содержат по 4 ядра. Числа 1, 3, 6, 10 называются “треугольными” числами.

Теперь представим себе пирамидальную кучу, составленную таким образом: на самом верху лежит одно ядро, под ним три, сложенные в треугольник,

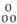
затем шесть, сложенные в треугольник

и так далее. Чтобы сразу узнать, сколько ядер в такой куче, достаточно посмотреть, какое число написано под последним взятым нами треугольным числом. В данном примере искомым является число 10, стоящее под числом 6. Числа 1, 4, 10 и т. д., составляющие четвертый ряд (или столбец), могут быть названы “пирамидальными”, потому что обозначают число ядер в пирамидальных кучах.