Яков Перельман - Занимательные опыты и задачи по физике

Еще основатель механики, Галилей, в XVII веке писал [3]: «Мы ощущаем груз на наших плечах, когда стараемся мешать его падению. Но если станем двигаться вниз с такой же скоростью, как и груз, лежащей на нашей спине, то как же может он давить и обременять нас? Это подобно тому, как если бы мы захотели поразить копьем [4]кого-либо, кто бежит впереди нас с такой же скоростью, с какой движемся и мы».

Следующий легко исполнимый опыт наглядно подтверждает правильность этих рассуждений.

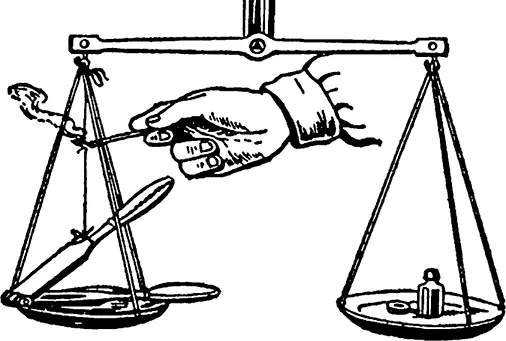
Рис. 24.Опыт, иллюстрирующий невесомость падающего тела.

На одну чашку торговых весов положите щипцы для раскалывания орехов так, чтобы одно колено их покоилось на чашке, другое же привяжите за конец ниткой к крючку коромысла (рис. 24). На другую чашку поместите столько груза, чтобы весы были в равновесии. Поднесите к нитке зажженную спичку; нитка перегорит и верхнее колено щипцов упадет на чашку.

Что же произойдет в этот момент с весами? Опустится ли чашка с щипцами в то время, пока колено еще падает, поднимется она или останется в равновесии?

Теперь, когда вы знаете уже, что падающее тело не имеет веса, вы можете заранее дать правильный ответ на этот вопрос: чашка должна подняться на мгновение вверх .

В самом деле: верхнее колено щипцов, падая, хотя и остается в соединении с нижним, все же давит на него меньше, чем в неподвижном состоянии. Вес щипцов на мгновение уменьшается, и чашка, естественно, поднимается вверх.

В 1865–1870 гг. появился во Франции фантастический роман Жюля Верна «Из пушки на Луну», в котором высказана необычайная мысль: послать на Луну исполинский пушечный снаряд-вагон с живыми людьми! Жюль Верн представил свой проект в столь правдоподобном виде, что у большинства читателей, наверное, возникал вопрос: нельзя ли в самом деле осуществить эту мысль? Об этом интересно побеседовать.

Сначала рассмотрим, можно ли – хотя бы теоретически – выстрелить из пушки так, чтобы снаряд никогда не упал назад, на Землю. Теория допускает такую возможность. В самом деле, почему снаряд, горизонтально выброшенный пушкой, в конце концов падает на Землю? Потому что Земля, притягивая снаряд, искривляет его путь: он летит не по прямой линии, а по кривой, направленной к Земле, и поэтому рано или поздно встречается с почвой. Земная поверхность, правда, тоже искривлена, но путь снаряда изгибается гораздо круче. Если же кривизну пути снаряда ослабить и сделать ее одинаковой с искривлением поверхности земного шара, то такой снаряд никогда не сможет упасть на Землю! Он будет двигаться по кривой, концентрической с окружностью земного шара; другими словами, сделается его спутником, как бы второй Луной.

Но как добиться, чтобы снаряд, выброшенный пушкой, шел по пути, менее искривленному, чем земная поверхность? Для этого необходимо только сообщить ему достаточную скорость. Обратите внимание на рис. 25, изображающий разрез части земного шара.

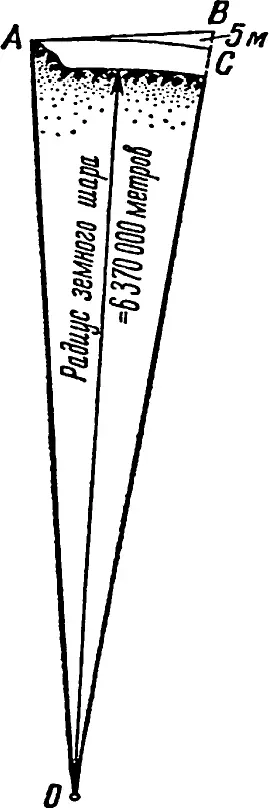
Рис. 25.Вычисление скорости снаряда, который должен навсегда покинуть Землю.

На горе, высотой которой будем пренебрегать, в точке A стоит пушка. Снаряд, горизонтально выброшенный ею, был бы через секунду в точке B , если бы не существовало притяжения Земли. Но притяжение меняет дело, и под действием этой силы снаряд через секунду окажется не в точке B , а на 5 м ниже, в точке C . Пять метров – это путь, проходимый (в пустоте) каждым свободно падающим телом в первую секунду под действием силы тяжести близ поверхности Земли. Если, опустившись на эти 5 м, снаряд наш окажется над уровнем Земли ровно настолько же, насколько был он в точке A , то, значит, он движется по кривой, концентрической с окружностью земного шара.

Остается вычислить отрезок АВ (рис. 25), т. е. тот путь, который проходит снаряд в секунду по горизонтальному направлению; мы узнаем тогда, с какой секундной скоростью нужно для нашей цели выбросить снаряд из жерла пушки. Вычислить это нетрудно из треугольника АОВ , в котором ОА – радиус земного шара (около 6 370 000 м); ОС = ОА, ВС = 5 м; следовательно, OВ = 6 370 005 м. Отсюда по теореме Пифагора имеем:

( AB )² = (6 370 005)² − (6 370 000)².

Сделав вычисление, находим, что путь AB равен примерно 8 км.